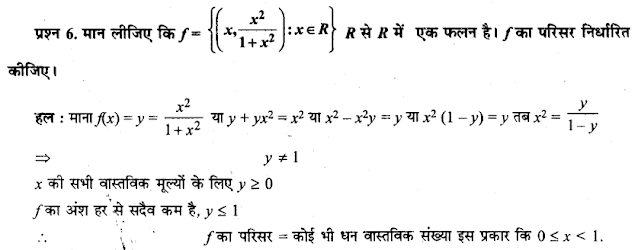NCERT Solutions Class 11 गणित-I Chapter-2 (संबंध एवं फलन)
Class 11 गणित-I
पाठ-2 (संबंध एवं फलन)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
Exercise 2.1
प्रश्न 2.
यदि समुच्चय A में 3 अवयव हैं तथा समुच्चय B = {3, 4, 5}, तो A x B में अवयवों की संख्या ज्ञात कीजिए।
हल:
समुच्चयं A में 3 अवयव है और समुच्चय B में भी 3 अवयव हैं।
A x B में अंवयवों की संख्या = 3 x 3 = 9.
प्रश्न 3.
यदि G = {7, 8} और H = {5, 4, 2}, तो G x H तथा H x G ज्ञात कीजिए।
हल:
G = {7, 8}, H = {5, 4, 2} G x H = {7, 8} x {5, 4, 2}
= {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}
तथा
H x G = {5, 4, 2} x {7, 8} = {(5, 7), (5, 8), (4,7), (4, 8), (2, 7), (2, 8)}
प्रश्न 4.
बताइए कि निम्नलिखित कथनों में से प्रत्येक सत्य है या असत्य है। यदि कथन असत्य है, तो दिए गए कथन को सही बनाकर लिखिए।
(i) यदि P= {m, n} और 2 = {n, m} तो P x Q = {(m, n), (n, m)}.
(ii) यदि A और B अरिक्त समुच्चय हैं, तो A x B क्रमित युग्मों (x, y) का एक अरिक्त समुच्यय है इस प्रकार कि x ∈ A तथा y ∈ B.
(iii) यदि A = {1, 2}, B = {3, 4}, तो A x (B ∩ Φ) = Φ
हल:
(i) दिया है :
P = {m, n}
Q = {n, m }
P x Q = {m, n} x {n, m} = {(m, n), (m, m), (n, n), (n, m)}
अतः दिया गया P x Q = {(m, n), (n, m),} कथन असत्य है।
(ii) सत्य है क्योंकि A x B क्रमित युग्म (x, y) का अरिक्त समुच्चय है जिसमें
x ∈ A तथा y ∈ B.
(iii) सत्य है क्योंकि B ∈ Φ = Φ
A x (B ⊂ Φ ) = A x Φ = Φ.
प्रश्न 5.
यदि A= {-1, 1}, तो A x A x A ज्ञात कीजिए।
हल:
A = {(-1, 1)}
A x A = {-1, 1} x {-1, 1} = {(-1,-1), (-1, 1), (1,- 1), (1,1)}
A x A x A = {-1, 1} x {(-1, – 1), (-1, 1), (1, -1), (1, 1)} = {(-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1), (1, 1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1)}.
प्रश्न 6.
यदि A x B = {(a, x), (a, y), (b, x), (b, y)} तो A तथा B ज्ञात कीजिए।
हल:
A x B = {(a, x), (a, y), (b, x), (b, y)} = {a, b} x {x, y}
अतः A = {a, b}, B = {x, y}.
प्रश्न 7.
मान लीजिए कि A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} तथा D = {5, 6, 7, 8} सत्यापित कीजिए कि
(i) A x (B ∩ C)= (A x B) ∩ (A x C)
(ii) A x C, B x D का एक उपसमुच्चय है।
हल:
दिया है। A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6}, D = {5, 6, 7, 8}
बायाँ पक्ष = A x (B ∩ C) {1, 2} x {{1, 2, 3, 4} ∩ {5, 6}) = {1, 2} x Φ = Φ
दायाँ पक्ष = (A x B) ∩ (A x C)
= [{1, 2} x {1, 2, 3, 4}] ∩ [{1, 2} { {5, 6}]
= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)} {(1, 5), (1, 6), (2, 5), (2, 6)}
= Φ
अतः बायाँ पक्ष = दायाँ पक्ष
A x C = {1, 2} x {5, 6} = {{1, 5), (1, 6), (2, 5), (2, 6)}
B x D = {1, 2, 3, 4} x {5, 6, 7, 8}
= {(1,5), (1,6), (1, 7), (1, 8), (2,5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
हम पाते हैं कि A x C के सभी अवयव समुच्चय B x D में स्थित हैं।
अतः A x C ⊂ B x D.
प्रश्न 8.
मान लीजिए कि A = {1, 2} और B = {3, 4}. A x B लिखिए। A x B के कितने उपसमुन्। होंगें ? उनकी सूची बनाइए।
हल:
A x B = {1, 2} x {3, 4} = {(1, 3), (1, 4), (2, 3), (2, 4)}
A x B के उपसमुच्चयों की संख्या = 24 = 16
A x B के उपसमुच्चयों के अवयव = 6, {(1, 3)}, {(1,4)}, {(2, 3)}, {(2, 4)}, {(1, 3), (1,4)}, {(1, 3)
(2, 3)},{(1, 3), (2, 4)}, {(1, 4), (2, 3)}, {(1, 4), (2,4)}, {(2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3)}, {(1, 3), (1, 4), (2, 4)}, {(1, 3), (2,3), (2, 4)}, {(1, 4), (2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3), (2, 4)}.
प्रश्न 9.
मान लीजिए कि A और B दो समुच्चय हैं, जहाँ n(A) = 3 और n(B) = 2. यदि (x, 1), (y, 2), (z, 1), A x B में हैं, तो A और B को ज्ञात कीजिए, जहाँ x, y और z भिन्न-भिन्न अवयव हैं।
हल:
अवयव x, y, z ∈ A अर्थात् A = {x, y, z}
1, 2 ∈ B अर्थात् B = {1, 2}.
प्रश्न 10.
कार्तीय गुणन AXA में 9 अवयव हैं जिनमें (-1, 0) तथा (0, 1) भी हैं। समुच्चय Aज्ञात कीजिए तथा A x A के शेष अवयव भी ज्ञात कीजिए।
हल:
(-1, 0) ∈ A x A ⇒ -1 ∈ A और 0 ∈ A ⇒ -1, 0 ∈ A और
(0, 1) ∈ A ⇒ 0 ∈ A तथा 1 ∈ A
⇒ 0, 1 ∈ A
-1, 0, 1 ∈ A
A = {-1, 0, 1}
A x A = {-1, 0, 1} x {-1, 0, 1}
= {(-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 0), (0, 1), (1,-1), (1,0), (1,1)}
जिसमें (-1, 0), (0, 1) सम्मिलित है।
अत: A x A के शेष अवयव = (-1, -1), (-1, 1), (0, -1), (0, 0), (1,- 1), (1, 0), (1, 1).
Exercise 2.2
प्रश्न 1.
मान लीजिए A = {1, 2, 3, …….14}, R = {x, y) : 3x – y = 0, जहाँ x, y ∈ A} द्वारा A से A का एक संबंध R लिखिए। इसके प्रांत, सहप्रांत और परिसर लिखिए।
हल:
A = {1, 2, 3, …., 14}, R : A जबकि
R = {(x, y) : 3x – y = 0 या y = 3x} = {(1, 3), (2, 6), (3, 9), (4, 12),….}
(i) प्रांत : संबंध R के समुच्चयों में x के अवयव = {1, 2, 3, 4}.
सहप्रांत : {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}.
परिसर : संबंध R के समुच्चयों में y के अवयव = {3, 6, 9, 12}.
प्रश्न 2.
प्राकृत संख्याओं के समुच्चय पर R = {x, y) : y = x + 5, x संख्या 4 से कम, एक प्राकृत संख्या है, x, y ∈ N} द्वारा एक संबंध R परिभाषित कीजिए। इस संबंध को
(i) रोस्टर रूप में इसके प्रांत और परिसर लिखिए।
हल:
संबंध R, दिया गया है।
R = {(x, y) : y = x + 5, x, y ∈ N तदा x < 4}
= {(1, 6), (2, 7), (3, 8)}
(i) प्रान्त = {1, 2, 3}.
परिसर = {6, 7, 8}.
प्रश्न 3.
A = {1, 2, 3, 5) और B = {4, 6, 9}, A से B में एक सम्बन्ध
R = {x, y} : x और y का अंतर विषम है, x ∈ A, y ∈ B} द्वार परिभाषित कीजिए| R को रोस्टर रूप में लिखिए।
हल:
दिया है:
A = {1, 2, 3, 5} और B = {4, 6, 9}. A से B में संबंध,
R = {(x, y) : x, y में अंतर विषम है, x ∈ A, y ∈ B}
= {1, 4,), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}.
प्रश्न 4.
दी हुई आकृति समुच्चय P से Q का एक संबंर दर्शाती है। इस संबंध को
(i) समुच्चय निर्माण रूप में
(ii) रोस्टर रूप में लिखिए। इसके प्रांत व परिसर क्या हैं ?
हल:
(i) समुच्चय निर्माण रूप में, R = {(3, y) : y = x – 2, x = 5, 6, 7 के लिए}
(ii) रोस्टर रूप में, R = {(5, 3), (6, 4), (7, 5)}
प्रान्त = {5, 6, 7}
और परिसर = {3, 4, 5}.
प्रश्न 5.
मान लीजिए कि A= {1, 2, 3, 4, 6} मान लीजिए कि R, A पर {(a, b) : a, b ∈ A, संख्या a संख्या b को यथावथ विभाजित करती है। द्वारा परिभाषित एक संबंध है।
(i) R को रोस्टर रूप में लिखिए।
(ii) R का प्रांत ज्ञात कीजिए।
(iii) R का परिसर ज्ञात कीजिए।
हल:
दिया है :
A = {1, 2, 3, 4, 6}
R = {(a, b) : a, b ∈ A, a संख्या b को विभाजित करती है।
(i) रोस्टर रूप में, R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}
(ii) R का प्रांत = {1, 2, 3, 4, 5, 6}
(iii) R का परिसर = {1, 2, 3, 4, 5, 6}.
प्रश्न 6.
R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}} द्वारा परिभाषित संबंध R के प्रांत और परिसर ज्ञात कीजिए।
हल:
R = {(x, x + 5) : x ∈ {, 1, 2, 3, 4, 5}} = {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}
R का प्रांत = {0, 1, 2, 3, 4, 5}
R का परिसर : {5, 6; 7, 8, 9, 10}.
प्रश्न 7.
संबंध R = {(x, x3) : x संख्या 10 से कम एक अभाज्य संख्या है। को रोस्टर रूप में लिखिए।
हल:
10 से कम अभाज्य संख्याएँ 2, 3, 5, 7
रोस्टर रूप में, R = {(x, x3) : x एक अभाज्य संख्या है जो 10 से कम है।
= {(2, 8), (3, 27), (5, 125), (7, 343)}.
प्रश्न 8.
मान लीजिए कि A= {x, y, z} और B = {1, 2}, A से B के संबंधों की संख्या ज्ञात कीजिए।
हल:
दिया है। A = {x, y, z}, B = {1, 2}
A x B = {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}
n(A x B) = 6
संबंधों की कुल संख्या = A x B के उपसमुच्चयों की संख्या = 26 = 64.
प्रश्न 9.
मान लीजिए कि R, Z पर, R= {(a, b) : a, b ∈ Z, a – b एक पूर्णाक है}, द्वारा परिभाषित एक संबंध है। R के प्रांत व परिसर ज्ञात कीजिए।
हल:
R समुच्चय Z पर एक संबंध है तथा R = {(a, b), a ∈ Z, b ∈ Z, a – b एक पूर्णांक संख्या है।
प्रांत (R) = Z
परिसर (R) = Z.
Exercise 2.3
प्रश्न 1.
निम्नलिखित संबंधों में से कौन से फलन हैं ? कारण का उल्लेख कीजिए। यदि संबंध एक फलन है तो उसका परिसर निर्धारित कीजिए।
(i) {(2,1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) {(1, 3), (1, 5), (2, 5)}
हल:
(i) माना R = {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
यह संबंध एक फलन है क्योंकि किसी भी दो क्रमित युग्म का पहला घटक बराबर नहीं है।
प्रान्त = {2, 6, 8, 11, 14, 17} तथा परिसर = {1}.
(ii) माना R = {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
यह एक फलन है क्योंकि किसी भी दो क्रमित युग्म का पहला घटक बराबर नहीं है।
अतः प्रांत = {2, 4, 6, 8, 10, 12, 14}, परिसर = {1, 2, 3, 4, 5, 6, 7}.
(iii) यह एक फलन नहीं है क्योंकि (1, 3), (1, 5) में पहला घटक समान है।
प्रश्न 2.
निम्नलिखित वास्तविक फलनों के प्रांत तथा परिसर ज्ञात कीजिए।
प्रश्न 3.
एक फलन f(x) = 2x – 5 द्वारा परिभाषित है। निम्नलिखित के मान लिखिए:
(i) f(0)
(ii) f(7)
(iii) f(-3)
हल:
f(x) = 2x – 5
(i) f(0) = 2 x 0 – 5 = -5
(ii) f(7) = 14 – 5 = 9
(iii) f(-3) = 2 x (-3) – 5 = – 6 – 5 = – 11.
प्रश्न 4.
फलन ‘t’ सेल्सियस तापमान का फारेनहाइट तापमान में प्रतिचित्रण करता है, जो t(C) = \frac { 9C }{ 5 }+ 32 द्वारा परिभाषित है। निम्नलिखित को ज्ञात कीजिए:
(i) t(0)
(ii) t(28)
(iii) t(-10)
(iv) C का मान, जब t(C) = 212
प्रश्न 5.
निम्नलिखित में से प्रत्येक फलन का परिसर ज्ञात कीजिए:
(i) f(x) = 2 – 3x, x ∈ R, x > 0.
(ii) f(x) = x² + 2, x एक वास्तविक संख्या है।
(iii) f(x) = x, एक वास्तविक संख्या है।
अध्याय 2 पर विविध प्रश्नावली
प्रश्न 8.
मान लीजिए कि f = {(1, 1), (2, 3), (0, -1), (-1, -3)} Z से Z में, f(x) = ax + b, द्वारा परिभाषित एक फलन है, जहाँ a, b कोई पूर्णाक हैं। a, b को निर्धारित कीजिए।
हल:
दिया है :
f = {(1, 1), (2, 3), (0, – 1), (-1, – 3)}
और f(x) = ax + b …..(A)
जब x = 1; y = 1, हो तब a + b = 1 …..(i)
और जबे x = 2, y = 3, 2a + b = 3 …..(ii)
समीकरण (i) और (ii) से,
a = 2, b = -1
a तथा b के इन मानों को समीकरण (A) में रखने पर,
f(x) = 2x – 1
जब x = 0, f(x) = -1
और जब x = -1, f(x) = -3
अतः f(x) = 2x – 1 तथा a = 2, b = -1.
प्रश्न 9.
R = {(a, b) : a, b ∈ N तथा a = b2} द्वारा परिभाषित N से N में, एक संबंध R है। क्या निम्नलिखित कथन सत्य है।
(i) {a, a} ∈ R सभी a ∈ N
(ii) (a, b) ∈ R का तात्पर्य है कि (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R का तात्पर्य है कि (a, c) ∈ R? प्रत्येक दशा में अपने उत्तर का औचित्य भी बताइए।
हल:
(i) a = a यह सत्य है जब a = 0, 0 ∉ N,
अत: यह एक संबंध नहीं है।
(ii) a = b2, और b = a2, यह a, b ∈ N, a, b के सभी मूल्यों के लिए सत्य नहीं है। अत: यह एक संबंध नहीं है।
(iii) जब a = b2, b = c2 तब a ≠ c2
यह संबंध नहीं है।
प्रश्न 10.
मान लीजिए A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} और f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}, क्या निम्नलिखित कथन सत्य है ?
(i) f, Aसे B में एक संबंध है।
(ii) f, A से B में एक फलन है। प्रत्येक दशा में अपने उत्तर का औचित्य बताइए।
हल:
(i) दिया है: A = {1, 2, 3, 4} तथा B = {1, 5, 9, 11, 15, 16}
A x B = {(1, 1), (1, 5), (1, 9), (1,11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11), (3, 15), (3,16), (4, 1), (4, 5), (4,9), (4, 11), (4, 15), (4, 16)}
अवयव, A x B का उपसमुच्चय है।
अतः यह एक संबंध है।
(ii) f में (2, 9) और (2, 11) अवयव प्रथम घटक दोनों युग्मों में 2 है।
यह फलन नहीं है।
प्रश्न 11.
मान लीजिए कि f, f = {(ab, a + b); a, b ∈ Z} द्वारा परिभाषित Z x Z का एक उपसमुच्चय है। क्या f, Z से Z में एक फलन है ? अपने उत्तर का औचित्य भी स्पष्ट कीजिए।
हल:
मान लीजिए a = 0, b = 1 हो, तब
ab = 0 और a + b = 0 + 1 = 1
पुनः माना a = 0, b = 2 हो, तब
ab = 0, a + b = 2.
अवयव 0 के दो प्रतिबिंब 1 और 2 हैं।
अत: f एक फलन नहीं है।
प्रश्न 12.
मान लीजिए कि A= {9, 10, 11, 12, 13} तथा f : A → N, f(n) = n का महत्तम अभाज्य गुणक द्वारा परिभाषित है।/का परिसर ज्ञात करो।
हल:
यदि n = 9 = 3 x 3 तो 3 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n= 10 = 2 x 5 तो 5 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n = 11 = 1 x 11 तो 11 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n = 12 = 22 x 3 तो 3 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n = 13 = 1 x 13 तो 13 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
अतः f का परिसर = {3, 5, 11, 13}.
एनसीईआरटी सोलूशन्स क्लास 11 गणित-I
- 1. सम्मुच्य
- 3. त्रिकोणमितीय फलन
- 4. गणितीय आगमन का सिद्धांत
- 5. सम्मिश्र संख्याएँ और द्विघातीय समीकरण
- 6. रैखिक असमिकाएँ
- 7. क्रमचय एवं संचय
- 8. द्विपद प्रमेय
- 9. अनुक्रम तथा श्रेणी