NCERT Solutions Class 12 Maths (Application Of Integrals) Miscellaneous Exercise
NCERT Solutions Class 12 Maths from class
12th Students will get the answers of
Chapter-8 (Application Of Integrals) Miscellaneous Exercise This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of
NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.
Q1. Find the area under the given curves and given lines: (i) y=x2,x=1,x=2 and x -axis (ii) y=x4,x=1,x=5 and x -axis
Answer. (i) The required area is represented by the shaded area ADCBA as 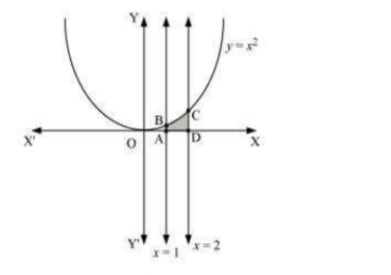 Area ADCBA=∫2ydx=∫x2dx=[x33]21=83−13=73 units (ii) The required area is represented by the shaded area ADCBA as
Area ADCBA=∫2ydx=∫x2dx=[x33]21=83−13=73 units (ii) The required area is represented by the shaded area ADCBA as 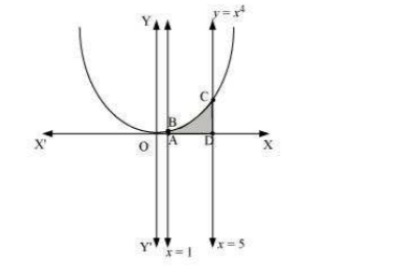 Area ADCBA=∫5x4dx=[x55]51=(5)55−15=(5)4−15=625−15=624.8 units
Area ADCBA=∫5x4dx=[x55]51=(5)55−15=(5)4−15=625−15=624.8 units
Q2. Find the area between the curve y=x and y=x2
Answer. The required area is represented by the shaded area OBAO as 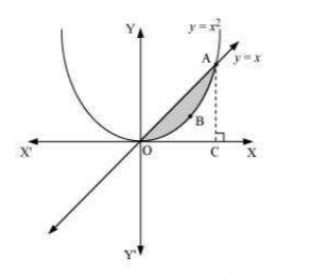 The points of intersection of the curves, y=x and y=x2, is A(1,1) . We draw AC perpendicular to x -axis. ∴ Area (OBAO)= Area (ΔOCA)− Area (OCABO) …(i) =∫xdx−∫t0x2dx=[x22]10−[x33]10=12−13=16 units
The points of intersection of the curves, y=x and y=x2, is A(1,1) . We draw AC perpendicular to x -axis. ∴ Area (OBAO)= Area (ΔOCA)− Area (OCABO) …(i) =∫xdx−∫t0x2dx=[x22]10−[x33]10=12−13=16 units
Q3. Find the area of the region lying in the first quadrant and bounded by y=4x2,x=0,y=1 and y=4
Answer. The area in the first quadrant bounded by y=4x2,x=0,y=1, and y=4 is represented by the shaded area ABCDA as 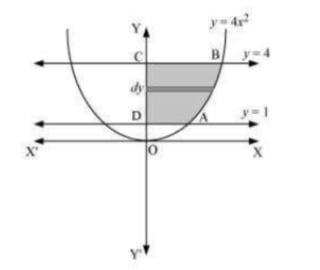 ∴ Area ABCD=∫1xxdx=∫√y2dx =12[y3232]4=13[(4)32−1]=13[8−1]=73 units
∴ Area ABCD=∫1xxdx=∫√y2dx =12[y3232]4=13[(4)32−1]=13[8−1]=73 units
Q4. Sketch the graph of y=|x+3| and evaluate ∫0−6|x+3|dx
Answer. The given equation is y=|x+3| The corresponding values of x and y are given in the following table. 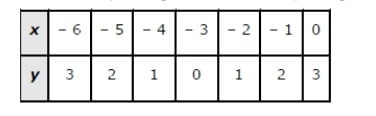 On plotting these points, we obtain the graph of y=|x+3| as follows.
On plotting these points, we obtain the graph of y=|x+3| as follows. 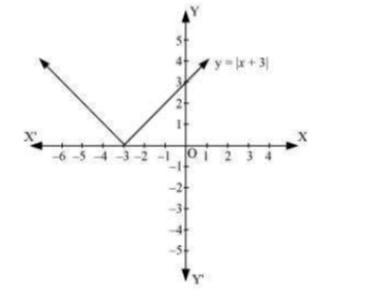 It is known that, (x+3)≤0 for −6≤x≤−3 and (x+3)≥0 for −3≤x≤0∴∫0−6(x+3)dx=−∫−3−6(x+3)dx+∫0−3(x+3)dx=−[x22+3x]−3−6+[x22+3x]0−3 =−[((−3)22+3(−3))−((−6)22+3(−6))]+[0−((−3)22+3(−3))]=−[−92]−[−92]=9
It is known that, (x+3)≤0 for −6≤x≤−3 and (x+3)≥0 for −3≤x≤0∴∫0−6(x+3)dx=−∫−3−6(x+3)dx+∫0−3(x+3)dx=−[x22+3x]−3−6+[x22+3x]0−3 =−[((−3)22+3(−3))−((−6)22+3(−6))]+[0−((−3)22+3(−3))]=−[−92]−[−92]=9
Q5. Find the area bounded by curve y=sinx between x=0 and x=2π
Answer. The graph of y = sin x can be drawn as 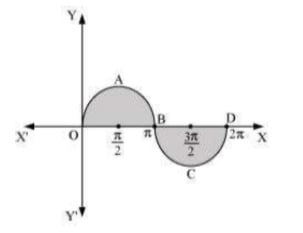 ∴ Required area = Area OABO + Area BCDB =∫π0sinxdx+∣∣∫2ππsinxdx∣∣=[−cosx]x0+|−cosx]2ππ|=[−cosπ+cos0]+|−cos2π+cosπ|=1+1+|(−1−1)|=2+|−2|=2+2=4 units
∴ Required area = Area OABO + Area BCDB =∫π0sinxdx+∣∣∫2ππsinxdx∣∣=[−cosx]x0+|−cosx]2ππ|=[−cosπ+cos0]+|−cos2π+cosπ|=1+1+|(−1−1)|=2+|−2|=2+2=4 units
Q6. Find the area enclosed between the parabola y2 = 4ax and the line y = mx
Answer. The area enclosed between the parabola, \(y^{2} = 4ax, and the line, y = mx, is represented by the shaded area OABO as 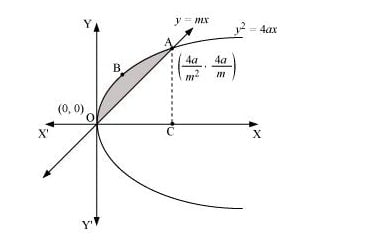 The points of intersection of both the curves are (0,0) and (4dm2,4am) we draw AC perpendicular to x -axis. ∴ Area OABO = Area OCABO – Area (ΔOCA)
The points of intersection of both the curves are (0,0) and (4dm2,4am) we draw AC perpendicular to x -axis. ∴ Area OABO = Area OCABO – Area (ΔOCA) 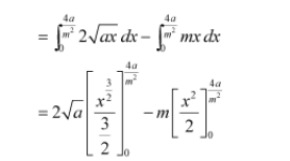 =43√a(4am2)32−m2[(4am2)2]=32a23m3−m2(16a2m4)=32a23m3−8a2m3=8a23m3 units
=43√a(4am2)32−m2[(4am2)2]=32a23m3−m2(16a2m4)=32a23m3−8a2m3=8a23m3 units
Q7. Find the area enclosed by the parabola 4y=3x2 and the line 2y=3x+12
Answer. The area enclosed between the parabola 4y=3x2 and the line 2y=3x+12 is represented by the shaded area OBAO as 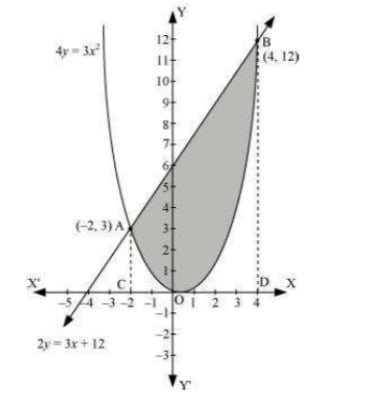 The points of intersection of the given curves are A (–2, 3) and (4, 12). We draw AC and BD perpendicular to x-axis. ∴ Area OBAO = Area CDBA – (Area ODBO + Area OACO) =∫4−212(3x+12)dx−∫1−23x24dx=12[3x22+12x]4−2−34[x33]4−2 =12[24+48−6+24]−14[64+8]=12[90]−14[72]=45−18=27 units
The points of intersection of the given curves are A (–2, 3) and (4, 12). We draw AC and BD perpendicular to x-axis. ∴ Area OBAO = Area CDBA – (Area ODBO + Area OACO) =∫4−212(3x+12)dx−∫1−23x24dx=12[3x22+12x]4−2−34[x33]4−2 =12[24+48−6+24]−14[64+8]=12[90]−14[72]=45−18=27 units
Q8. Find the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1
Answer. The area of the smaller region bounded by the ellipse, x29+y24=1 and the line, x3+y2=1 is represented by the shaded region BCAB as 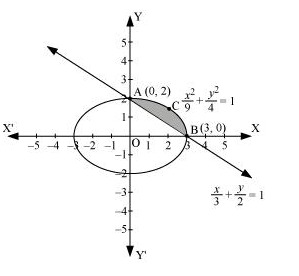 ∴ Area BCAB = Area (OBCAO) – Area (OBAO) =∫302√1−x29dx−∫302(1−x3)dx=23[∫30√9−x2dx]−23∫30(3−x)dx=23[x2√9−x2+92sin−1x3]30−23[3x−x22]30 =23[92(π2)]−23[9−92]=23[9π4−92]=23×94(π−2)=32(π−2) units
∴ Area BCAB = Area (OBCAO) – Area (OBAO) =∫302√1−x29dx−∫302(1−x3)dx=23[∫30√9−x2dx]−23∫30(3−x)dx=23[x2√9−x2+92sin−1x3]30−23[3x−x22]30 =23[92(π2)]−23[9−92]=23[9π4−92]=23×94(π−2)=32(π−2) units
Q9. Find the area of the smaller region bounded by the Find the area of the smaller region bounded by the ellipse x2a2+y2b2=1 and the line xa+yb=1
Answer. The area of the smaller region bounded by the ellipse, x2a2+y2b2=1 and the line xa+yb=1 is represented by the shaded region BCAB as 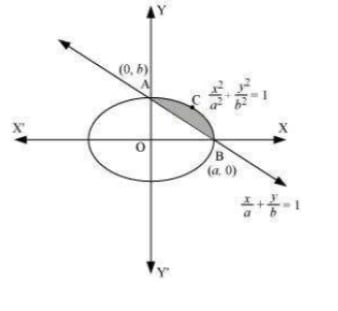 ∴ Area BCAB = Area (OBCAO) – Area (OBAO) =∫a0b√1−x2a2dx−∫abb(1−xa)dx=ba∫00√a2−x2dx−ba∫a0(a−x)dx =ba[{x2√a2−x2+a22sin−1xa}a0−{ax−x22}a0]=ba[{a22(π2)}−{a2−a22}]=ba[a2π4−a22]
∴ Area BCAB = Area (OBCAO) – Area (OBAO) =∫a0b√1−x2a2dx−∫abb(1−xa)dx=ba∫00√a2−x2dx−ba∫a0(a−x)dx =ba[{x2√a2−x2+a22sin−1xa}a0−{ax−x22}a0]=ba[{a22(π2)}−{a2−a22}]=ba[a2π4−a22]
Q10. Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and x-axis
Answer. The area of the region enclosed by the parabola, x2 = y, the line, y = x + 2, and x-axis is represented by the shaded region OACO as 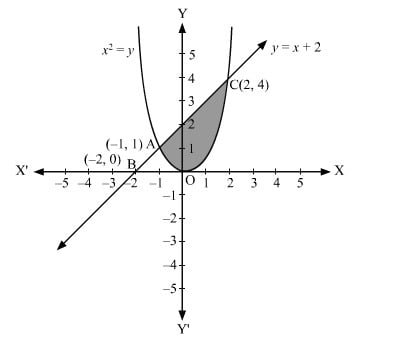 The point of intersection of the parabola, x2=y, and the line, y=x+2, is A(−1,1) . ∴ Area OABCO = Area (BCA)+ Area COAC =∫12(x+2)dx+∫0−1x2dx=[x22+2x]−1−2+[x33]0−1=[(−1)22+2(−1)−(−2)22−2(−2)]+[−(−1)33]=[12−2−2+4+13]=56 units
The point of intersection of the parabola, x2=y, and the line, y=x+2, is A(−1,1) . ∴ Area OABCO = Area (BCA)+ Area COAC =∫12(x+2)dx+∫0−1x2dx=[x22+2x]−1−2+[x33]0−1=[(−1)22+2(−1)−(−2)22−2(−2)]+[−(−1)33]=[12−2−2+4+13]=56 units
Q11. Using the method of integration find the area bounded by the curve |x|+|y|=1 [Hint: the required region is bounded by lines x+y=1,x−y=1,−x+y=1 and −x−y=11]
Answer. The area bounded by the curve, |x|+|y|=1 , is represented by the shaded region ADCB as 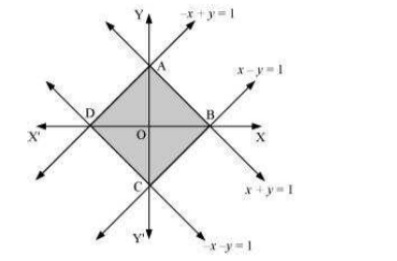 The curve intersects the axes at points A (0, 1), B (1, 0), C (0, –1), and D (–1, 0). It can be observed that the given curve is symmetrical about x-axis and y-axis. ∴ Area ADCB = 4 × Area OBAO =4∫d0(1−x)dx=4(x−x22)1=4[1−12]0=4(12)=2 units
The curve intersects the axes at points A (0, 1), B (1, 0), C (0, –1), and D (–1, 0). It can be observed that the given curve is symmetrical about x-axis and y-axis. ∴ Area ADCB = 4 × Area OBAO =4∫d0(1−x)dx=4(x−x22)1=4[1−12]0=4(12)=2 units
Q12. Find the area bounded by curves {(x,y):y≥x2 and y=|x|}
Answer. The area bounded by the curves, {(x,y):y≥x2 and y=|x|}, is represented by the shaded region as 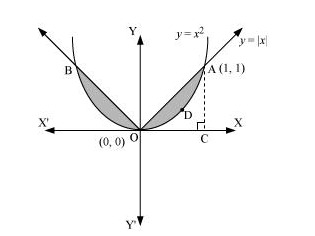 It can be observed that the required area is symmetrical about y-axis. Required area =2[ Area (OCAO)− Area (OCADO ) ]=2[∫xdx−∫x2dx]=2[[x22]10−[x33]10]=2[12−13]=2[16]=13 units
It can be observed that the required area is symmetrical about y-axis. Required area =2[ Area (OCAO)− Area (OCADO ) ]=2[∫xdx−∫x2dx]=2[[x22]10−[x33]10]=2[12−13]=2[16]=13 units
Q13. Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A (2, 0), B (4, 5) and C (6, 3)
Answer. The vertices of ΔABC are A (2, 0), B (4, 5), and C (6, 3). 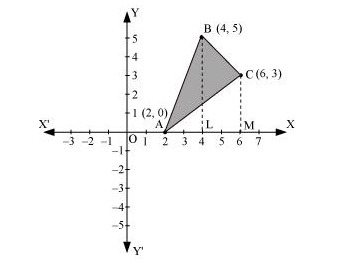 Equation of line segment AB is Equation of line segment AB is y−0=5−04−2(x−2)2y=5x−10y=52(x−2) ...(i) Equation of line segment BC is y−5=3−56−4(x−4)2y−10=−2x+82y=−2x+18y=−x+9 ...(ii) Equation of line segment ca is y−3=0−32−6(x−6)−4y+12=−3x+18y=34(x−2) ...(iii) Area (ΔABC) = Area (ABLA) + Area (BLMCB) – Area (ACMA) =∫4252(x−2)dx+∫64(−x+9)dx−∫6234(x−2)dx=52[x22−2x]42+[−x22+9x]64−34[x22−2x]62=52[8−8−2+4]+[−18+54+8−36]−34[18−12−2+4]=5+8−34(8)=13−6=7 units
Equation of line segment AB is Equation of line segment AB is y−0=5−04−2(x−2)2y=5x−10y=52(x−2) ...(i) Equation of line segment BC is y−5=3−56−4(x−4)2y−10=−2x+82y=−2x+18y=−x+9 ...(ii) Equation of line segment ca is y−3=0−32−6(x−6)−4y+12=−3x+18y=34(x−2) ...(iii) Area (ΔABC) = Area (ABLA) + Area (BLMCB) – Area (ACMA) =∫4252(x−2)dx+∫64(−x+9)dx−∫6234(x−2)dx=52[x22−2x]42+[−x22+9x]64−34[x22−2x]62=52[8−8−2+4]+[−18+54+8−36]−34[18−12−2+4]=5+8−34(8)=13−6=7 units Q14. Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Answer. The given equations of lines are 2x + y = 4 … (i) 3x – 2y = 6 … (ii) And, x – 3y + 5 = 0 … (iii) 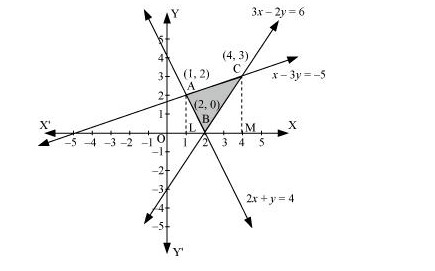 The area of the region bounded by the lines is the area of ΔABC. AL and CM are the perpendiculars on x-axis. Area (ΔABC) = Area (ALMCA) – Area (ALB) – Area (CMB) =∫4(x+53)dx−∫2(4−2x)dx−∫42(3x−62)dx=13[x22+5x]41−[4x−x2]21−12[3x22−6x]42=13[8+20−12−5]−[8−4−4+1]−12[24−24−6+12]=(13×452)−(1)−12(6)=152−1−3=152−4=15−82=72 units
The area of the region bounded by the lines is the area of ΔABC. AL and CM are the perpendiculars on x-axis. Area (ΔABC) = Area (ALMCA) – Area (ALB) – Area (CMB) =∫4(x+53)dx−∫2(4−2x)dx−∫42(3x−62)dx=13[x22+5x]41−[4x−x2]21−12[3x22−6x]42=13[8+20−12−5]−[8−4−4+1]−12[24−24−6+12]=(13×452)−(1)−12(6)=152−1−3=152−4=15−82=72 units
Q15. Find the area of the region {(x,y):y2≤4x,4x2+4y2≤9}
Answer. The area bounded by the curves, {(x,y):y2≤4x,4x2+4y2≤9} is represented as 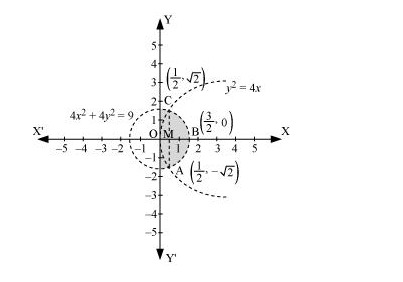 The points of intersection of both the curves are (12,√2) and (12,−√2) The required area is given by OABCO. It can be observed that area OABCO is symmetrical about x-axis. ∴ Area OABCO = 2 × Area OBC Area OBCO = Area OMC + Area MBC =∫102√xdx+∫321212√9−4x2dx=∫102√xdx+∫321212√(3)2−(2x)2dx
The points of intersection of both the curves are (12,√2) and (12,−√2) The required area is given by OABCO. It can be observed that area OABCO is symmetrical about x-axis. ∴ Area OABCO = 2 × Area OBC Area OBCO = Area OMC + Area MBC =∫102√xdx+∫321212√9−4x2dx=∫102√xdx+∫321212√(3)2−(2x)2dx
Q16. Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is A. −9 B. −154 B. 154 D. 174
Answer. 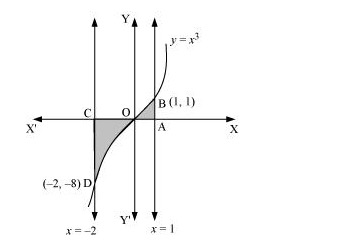 Required area =∫12ydx=∫12x3dx=[x44]1−2=[14−(−2)44]=(14−4)=−154 units =(14−4)=−154 units Thus, the correct answer is B.
Required area =∫12ydx=∫12x3dx=[x44]1−2=[14−(−2)44]=(14−4)=−154 units =(14−4)=−154 units Thus, the correct answer is B.
Q17. The area bounded by the curve y=x|x|,x -axis and the ordinates x=−1 and x=1 is given by [Hint: y=x2 if x>0 and y=−x2 if x<0] A. 0 B. 13 C. 23 D. 43
Answer. 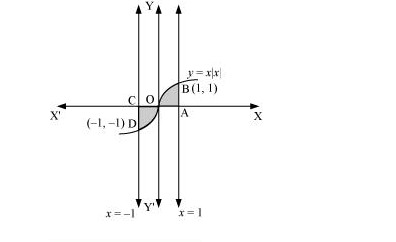 Required area =∫1−1ydx=∫∞−1x|x|dx=∫0−1x2dx+∫10x2dx=[x33]0−1+[x33]10=−23 units =23 units Thus, the correct answer is C.
Required area =∫1−1ydx=∫∞−1x|x|dx=∫0−1x2dx+∫10x2dx=[x33]0−1+[x33]10=−23 units =23 units Thus, the correct answer is C.
Q18. The area of the circle x2+y2=16 exterior to the parabola y2=6x (A) 43(4π−√3) (B) 43(4π+√3) (C) 43(8π−√3) (D) 43(8π+√3)
Answer. The given equations are x2+y2=16…(i)y2=6x…(ii) 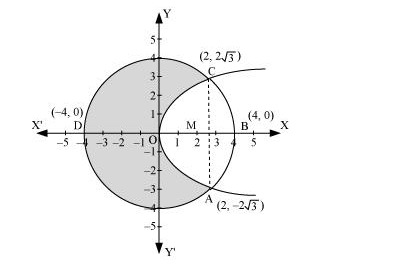 Area bounded by the circle and parabola =2[Arca(OADO)+Area(ADBA)]=2[∫20√16xdx+∫+2√16−x2dx]=2⎡⎣√6{x322}20⎤⎦+2[x2√16−x2+162sin−1x4]42=2√6×23[x32]20+2[8⋅π2−√16−4−8sin−1(12)] =4√63(2√2)+2[4π−√12−8π6]=16√33+8π−4√3−83π=43[4√3+6π−3√3−2π]=43[√3+4π] Area of circle =n(r)2=16n units ∴ Required area =16π−43[4π+√3]=43[4×3π−4π−√3]=43(8π−√3) units Thus, the correct answer is C
Area bounded by the circle and parabola =2[Arca(OADO)+Area(ADBA)]=2[∫20√16xdx+∫+2√16−x2dx]=2⎡⎣√6{x322}20⎤⎦+2[x2√16−x2+162sin−1x4]42=2√6×23[x32]20+2[8⋅π2−√16−4−8sin−1(12)] =4√63(2√2)+2[4π−√12−8π6]=16√33+8π−4√3−83π=43[4√3+6π−3√3−2π]=43[√3+4π] Area of circle =n(r)2=16n units ∴ Required area =16π−43[4π+√3]=43[4×3π−4π−√3]=43(8π−√3) units Thus, the correct answer is C
Q19. The area bounded by the y-axis, y = cos x and y = sin x When 0≤x≤π2. A. 2(√2−1) B. √2−1 C. √2+1 D. √2
Answer. The given equations are y = cos x … (i) And, y = sin x … (ii) 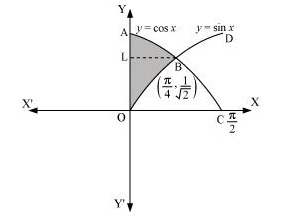 Required area = Area (ABLA) + area (OBLO) =∫41xdy+∫10xdy=∫d1cos−1ydy+∫120sin−1xdy Integrating by parts, we obtain =[ycos−1y−√1−y2]11√2+[xsin−1x+√1−x2]1√20=[cos−1(1)−1√2cos−1(1√2)+√1−12]+[1√2sin−1(1√2)+√1−12−1]=−π4√2+1√2+π4√2+1√2−1=2√2−1=√2−1 units Thus, the correct answer is B. Put 2x=t⇒dx=dt2 When x=32,t=3 and when x=12,t=1=∫1202√xdx+14∫31√(3)2−(t)2dt =2[x322]12+14[t2√9−t2+92sin−1(t3)]31=2[23(12)32]+14[{32√9−(3)2+92sin−1(33)}−{12√9−(1)2+92sin−1(13)}] =23√2+14[{0+92sin−1(1)}−{12√8+92sin−1(13)}]=√23+14[9π4−√2−92sin−1(13)]=√23+9π16−√24−98sin−1(13)=9π16−98sin−1(13)+√212 Therefore , the required area is [2×(9π16−98sin−1(13)+√212)]=9π8−94sin−1(13)+13√2 units
Required area = Area (ABLA) + area (OBLO) =∫41xdy+∫10xdy=∫d1cos−1ydy+∫120sin−1xdy Integrating by parts, we obtain =[ycos−1y−√1−y2]11√2+[xsin−1x+√1−x2]1√20=[cos−1(1)−1√2cos−1(1√2)+√1−12]+[1√2sin−1(1√2)+√1−12−1]=−π4√2+1√2+π4√2+1√2−1=2√2−1=√2−1 units Thus, the correct answer is B. Put 2x=t⇒dx=dt2 When x=32,t=3 and when x=12,t=1=∫1202√xdx+14∫31√(3)2−(t)2dt =2[x322]12+14[t2√9−t2+92sin−1(t3)]31=2[23(12)32]+14[{32√9−(3)2+92sin−1(33)}−{12√9−(1)2+92sin−1(13)}] =23√2+14[{0+92sin−1(1)}−{12√8+92sin−1(13)}]=√23+14[9π4−√2−92sin−1(13)]=√23+9π16−√24−98sin−1(13)=9π16−98sin−1(13)+√212 Therefore , the required area is [2×(9π16−98sin−1(13)+√212)]=9π8−94sin−1(13)+13√2 units
 (ii) The required area is represented by the shaded area ADCBA as
(ii) The required area is represented by the shaded area ADCBA as 


 On plotting these points, we obtain the graph of as follows.
On plotting these points, we obtain the graph of as follows. 
 ∴ Required area = Area OABO + Area BCDB
∴ Required area = Area OABO + Area BCDB  ∴ Area OABO = Area OCABO – Area (ΔOCA)
∴ Area OABO = Area OCABO – Area (ΔOCA) 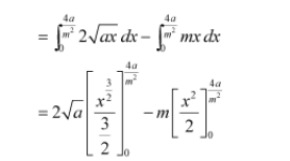
 The points of intersection of the given curves are A (–2, 3) and (4, 12). We draw AC and BD perpendicular to x-axis. ∴ Area OBAO = Area CDBA – (Area ODBO + Area OACO)
The points of intersection of the given curves are A (–2, 3) and (4, 12). We draw AC and BD perpendicular to x-axis. ∴ Area OBAO = Area CDBA – (Area ODBO + Area OACO)  ∴ Area BCAB = Area (OBCAO) – Area (OBAO)
∴ Area BCAB = Area (OBCAO) – Area (OBAO)  ∴ Area BCAB = Area (OBCAO) – Area (OBAO)
∴ Area BCAB = Area (OBCAO) – Area (OBAO) 
 The curve intersects the axes at points A (0, 1), B (1, 0), C (0, –1), and D (–1, 0). It can be observed that the given curve is symmetrical about x-axis and y-axis. ∴ Area ADCB = 4 × Area OBAO
The curve intersects the axes at points A (0, 1), B (1, 0), C (0, –1), and D (–1, 0). It can be observed that the given curve is symmetrical about x-axis and y-axis. ∴ Area ADCB = 4 × Area OBAO  It can be observed that the required area is symmetrical about y-axis.
It can be observed that the required area is symmetrical about y-axis.  Equation of line segment AB is Area (ΔABC) = Area (ABLA) + Area (BLMCB) – Area (ACMA)
Equation of line segment AB is Area (ΔABC) = Area (ABLA) + Area (BLMCB) – Area (ACMA)  The area of the region bounded by the lines is the area of ΔABC. AL and CM are the perpendiculars on x-axis. Area (ΔABC) = Area (ALMCA) – Area (ALB) – Area (CMB)
The area of the region bounded by the lines is the area of ΔABC. AL and CM are the perpendiculars on x-axis. Area (ΔABC) = Area (ALMCA) – Area (ALB) – Area (CMB)  The points of intersection of both the curves are The required area is given by OABCO. It can be observed that area OABCO is symmetrical about x-axis. ∴ Area OABCO = 2 × Area OBC Area OBCO = Area OMC + Area MBC
The points of intersection of both the curves are The required area is given by OABCO. It can be observed that area OABCO is symmetrical about x-axis. ∴ Area OABCO = 2 × Area OBC Area OBCO = Area OMC + Area MBC 
 Thus, the correct answer is C.
Thus, the correct answer is C. Area bounded by the circle and parabola
Area bounded by the circle and parabola  Required area = Area (ABLA) + area (OBLO) Therefore , the required area is units
Required area = Area (ABLA) + area (OBLO) Therefore , the required area is units









