NCERT Solutions Class 12 Physics Chapter-1 (Electric Charges and Fields)
NCERT Solutions Class 12 Physics from class 12th Students will get the answers of Chapter-1 (Electric Charges and Fields) This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of NCERT Board Physics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.

NCERT Question-Answer
Class 12 Physics
Chapter-1 (Electric Charges and Fields)
Questions and answers given in practice
Chapter-1 (Electric Charges and Fields)
Question 1.
What is the force between two small charged spheres having charges of 2 x 10-7 C and 3 x 10-7 C placed 30 cm apart in the air?
Question 2.
The electrostatic force on a small sphere of charge 0.4 μC due to another small sphere of charge -0.8 μC in air is 0.2 N.
(a) What is the distance between the two spheres?
(b) What is the force on the second sphere due to the first?
Answer:
(a) Force on charge 1 due to charge 2 is given by the relation%20(42).png)
Question 3.
Check that the ratio ke2/G memp. is dimensionless. Lookup a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
Answer:%20(41).png)
Thus, the given ratio is a number and is dimensionless. This ratio signifies that electrostatic force between electron and proton is very-very large as compared to the gravitational force between them.
Question 4.
(a) Explain the meaning of the statement ‘electric charge of a body is quantised.’
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic i.e., large-scale charges?
Answer:
(a) Charge occurs in nature as a discrete entity. One packet of charge (least quantity) is called quantum charge. It is represented by ‘e‘. Generally, charge of an electron is represented by ‘e’ and charge of a proton is represented by ‘+ e’. Therefore, the charge possessed by any charged body will be an integral multiple of ± e, ie., ne where n = 1, 2, 3,
∴ q = ± ne
The fact that electric charge collections are integral multiples of the fundamental electronic charge was proved experimentally by Millikan.
(b) While dealing with the large-scale electrical phenomenon, we ignore the quantization of charge because the magnitude of charge of proton and electron is so small. For continuous charge distribution, charge can be accounted in terms of charge density such as linear charge density λ etc. We need not go for individual charges.
Question 5.
When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
Answer:
Before rubbing, both the glass rod and the silk cloth are electrically neutral. In other words, the net charge on the glass rod and the silk cloth is zero. When the glass rod is rubbed with silk cloth, a few electrons from the glass rod get transferred to the silk cloth. As a result, the glass rod becomes positively charged and the silk cloth negatively charged. Since the magnitude of positive charge on the glass rod is the same as that of negative charge on the silk, the net charge on the system is zero. Thus the appearances of charge on the glass rod and the silk cloth is in accordance with the law of conservation of charges.
Question 6.
Four-point charges qA = 2 μC, qB = -5 μC, or qc = -2 μC and qD = -5 μC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1μC placed at the center of the Square?
Answer:
The symmetry of the figure clearly indicates that 1μC charge will experience equal and opposite forces due to equal charges of 2μC placed at A and C. Similarly, 1μC charge will experience equal and opposite forces due to -5 μC charges placed at D and B.%20(40).png)
Thus, net force = zero.
Question 7.
(a) An electrostatic field line is a continuous curve.
That is, a field line cannot have sudden breaks. Why not?
(b) Explain why two field lines never cross each other at any point?
Answer:
(a) Electric lines of force exist throughout the region of an electric field. The electric field of a charge decreases gradually with increasing distance from it and becomes zero at infinity (i)e., electric field can’t vanish abruptly. So a line of force can’t have sudden breaks, it must be a continuous curve.
(b) If two lines of force intersect, then there would be two tangents and hence two directions of electric fields at the point of intersection, which is not possible.
Question 8.
Two-point charges qA = 3μC and qB = -3 μC are located 20 cm apart in vacuum.
(a) What is the electric field at the midpoint O of the line AB joining the two charges?
(b) If a negative test charge of magnitude 1.5 x 10-9 C is placed at this point, what is the force experienced by the test charge?
Answer:
(a) Electric field at the midpoint of the separation between two equal and opposite charges is given by%20(39).png)
%20(38).png)
(b) Force experienced by test charge = q0E
= (1.5 x 10-9) (5.4 x 106)
= 8.1 x 10-3 N along BA
Question 9.
A system has two charges qA = 2.5 x 10-7 C and qB = -2.5 x 10-7 C located at points
A : (0,0, -15 cm) and B : (0, 0, + 15 cm), respectively. What are the total charge and electric dipole moments of the system?
Answer:
Clearly, the given points are lying on the z-axis.
Distance between charges, 21%20(36).png)
= 15 + 15 = 30 cm = 0.3 m
Total charge = (2.5 x 10-7) – (2.5 x 10-7) = 0
Dipole moment
= q x 21 = 2.5 x 10-7 x 0.3
= 7.5 x 10-8 C m along negative z-axis.
Question 10.
An electric dipole with dipole moment 4 x 10-9 Cm is aligned at 30° with the direction of a uniform electric field of magnitude 5 x 104 NC-1. Calculate the magnitude of the torque acting on the dipole.
Answer:
Using τ = pE sin 0, we get
= (4 x 10-9) (5x 10-4 sin 30°)
= 2 x 10-4 x .png)
Question 11.
A polythene piece rubbed with wool is found to have a negative charge of 3.2 x 10-4 C.
(a) (Estimate the number of electrons transferred (from which to which ?)
(b) Is there a transfer of mass from wool to polythene?
Answer:
(a) Using q = ne, we get%20(35).png)
(b) Yes, but of negligible amount because mass of an electron is very-very small (mass transferred = me x n = 91 x 10-31 x 2 x 1012 = 1.82 x 10-18 kg).
Question 12.
(a) Two insulated charged copper spheres A and B have their centers separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5 x 10–7 C ? The radii of A and B are negligible compared to the distance of separation.
(b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?
Answer:%20(34).png)
Question 13.
Suppose the spheres A and B in Q 1.12 have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second, and finally removed from both. What is the new force of repulsion between A and B?
Answer:
Charge on sphere A on contact with the third sphere (say C) having no charge is given by%20(33).png)
When third sphere, how having charge 3.25 10-7 C is brought in contact with sphere B, the charge left on sphere B is given by,%20(32).png)
Question 14.
Figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?%20(30).png)
Answer:
Unlike charges attract each other, therefore particle 1 and 2 are negatively charged whereas particle 3 has a positive charge. Particle 3 gets maximum deflection so it has the highest charge (e) to mass (m) ratio because deflection, y α e/m
Consider a uniform electric field
%20(2).png)
= 3 x 103
%20(3).png) N/C.
N/C.(a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane?
(b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
Answer:
(a) Electric flux through the square,%20(29).png)
Question 16.
What is the net flux of the uniform electric field of Problem 1.15 through a cube of the side 20 cm oriented so that its faces are parallel to the coordinate planes?
Answer:
Zero, because the number of field lines entering the cube is equal to the number of field lines coming out of the cube.
Question 17.
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 x 103 Nm2/C.
Answer:
(a) What is the net charge inside the box?
(b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or why not?
Ans.
(a) Using φ = φ /ε0 we get q =φ ε0
= (8 x 103) (8.854 x 10-12)
= 70.8 x 10-9 C = 0.07 μC
(b) No, it cannot be said so because there may be an equal number of positive and negative elementary changes inside the box. It can only be said that the net charge inside the box is zero.
Question 18.
A point charge + 10 μC is a distance 5 cm directly above the center of a square of side 10 cm, as shown in the given figure. What is the magnitude of the electric flux through the square? [Hint. Think of the square as one fact of a cube with edge 10 cm.]%20(28).png)
Answer:
The charge can be assumed to be placed as shown in the figure.%20(27).png)
Question 19.
A point charge of 2.0 μC is at the center of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
Answer:%20(26).png)
Question 20.
A point charge causes an electric flux of -1.0 x 103 Nm2/C to pass through a spherical Gaussian surface of a 10.0 cm radius centered on the charge.
(a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface?
(b) What is the value of the point charge?
Answer:
(a) The electric flux depends only on the charge enclosed by the Gaussian surface and independent of the size of the Gaussian surface. The electric flux through new Gaussian surface remains same
i.e. -1 x 103 Nm2 C-1 because the charge enclosed remains same in this case also.
(b) Using φ = q/ε0, we get q = ε0 φ = (8.85 x 10-12) (-1 x 103)
i.e. q = -8.85 x 10-9 C.
Question 21.
a conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the center of the sphere is 1.5 x 103 N/C and points radially inward, what is the net charge on the sphere?
Answer:%20(25).png)
Question 22.
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.4 μC /m2.
(a) Find the charge on the sphere.
(b) What is the total electric flux leaving the surface of the sphere?
Answer:
(a) Charge on the sphere is given by%20(24).png)
Question 23.
An infinite line charge produces a field of 9 X 104 N/C at a distance of 2 cm. Calculate the linear charge density
Answer:%20(23).png)
Question 24.
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 x 10-22 C/m2. What is E?%20(22).png)
(a) in the outer region of the first plate,
(b) in the outer region of the second plate, and
(c) between the plates?
Answer:%20(21).png)
Question 25.
An oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55 x 104 NC-1 in Millikan’s oil drop experiment. The density of the oil is 1.26 g cm-3. Estimate the radius of the drop, (g = 9.81 ms-2 ; e = 1.60 x 10-19 C.)
Answer:
Charge on the drop,%20(20).png)
Question 26.
Which among the curves shown in the figure cannot possibly represent electrostatic field lines?%20(19).png)
%20(18).png)
%20(17).png)
Answer:
(a) Incorrect, because the field lines should be normal to the surface of a conductor.
(b) Incorrect, because the field lines cannot start from a negative charge.
(c) Correct
(c) Incorrect, because electric field lines cannot intersect with each other.
(d) Incorrect, because electrostatic field lines cannot form a closed loop.
Question 27.
In a certain region of space, the electric field is along the z-direction throughout. The magnitude of the electric field is, however, not constant but increases uniformly along the positive z-direction, at the rate of 105 N C-1 per meter. What are the force and torque experienced by a system having a total dipole moment equal to 10-7 C m in the negative z-direction?
Answer:
Suppose the dipole is along the z-axis.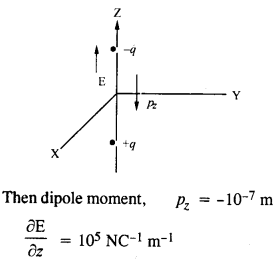
%20(15).png)
Question 28.
(a) A conductor A with a cavity as shown in figure (a) is given a charge Q. Show that the entire charge must appear on the outer surface of the conductor.
(b) Another conductor B with charge q is inserted into the cavity keeping B insulated from A. Show that the total charge on the outside surface of A is Q + q [Figure (b)].
(c) A sensitive instrument is to be shielded from the strong electrostatic fields in its environment. Suggest a possible way.%20(14).png)
Answer:
Select a Gaussian surface lying wholly inside the conductor but very near to the surface of the conductor.
(a) There is no electric field inside the conductor so electric flux through Gaussian surface is zero or in other words, net charge inside the Gaussian surface is zero. Then it can be said that the charge lies outside the Gaussian surface e. on the outer surface of the conductor.
(b) Charge q inside the cavity will induce a charge -q on the inner side of the cavity and thus +q will appear on the outer surface. Thus total charge will be (q + Q).
(c) The instrument should be enclosed in a metallic shell so that the effect of the electrostatic field is cancelled out.
Question 29.
A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is (σ/2ε0) .png) ,
, .png) where
where
Answer:
Let the tiny hole of the conductor be considered as filled up. The field inside the conductor is zero, whereas outside it is given by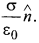
This field is infact due to
(1) field (E1) due to plugged hole and
(2) field E2 due to rest of the charged conductor. Inside the conductor, these fields are equal but opposite, whereas outside they are exactly same. i.e.%20(13).png)
Question 30.
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density X without using Gauss’s law.
[Hint. Use Coulomb’s law directly and evaluate the necessary integral.]
Answer:
Consider a long thin wire of uniform linear charge density X placed along the X-axis. Let P be a point lying on the y-axis%20(12).png)
%20(10).png)
%20(9).png)
%20(7).png)
%20(6).png)
Question 31.
It is now believed that protons and neutrons (which constitute nuclei of ordinary matter) are themselves build-out of more elementary units called quarks. A proton and a neutron consist of three quarks each. Two types of quarks, the so called ‘up’ quark (denoted by u) of charge + (2/3)e, and the ‘down’ quark (denoted by d) of charge
(-l/3)e, together with electrons build up ordinary matter. (Quarks of other types have also been found which give rise to different unusual varieties of matter.) Suggest a possible quark composition of a proton and neutron.)
Answer:%20(5).png)
Question 32.
(a) Consider an arbitrary electrostatic field configuration. A small test charge is placed at a null point (i.e., where E = 0) of the configuration. Show that the equilibrium of the test charge is necessarily unstable.
(b) Verify this result for the simple configuration of two charges of the same magnitude and sign placed a certain distance apart.
Answer:
(a) To prove the result, let us assume that the test charge placed at the null point is in stable equilibrium. If it is so, then on being displaced slightly away from the null point, the test charge should return to its position., It implies that if a closed surface is drawn around the test charge, there will be a net inward flux of the electric field through its surface. According to Gauss law, there cannot be any electric flux through its surface as it does not enclose any charge. Hence our assumption is wrong and the test
(b) For the configuration of the two charges of the same magnitude and sign, the null point is the midpoint of the line joining the two charges. If the test charge is displaced slightly from the null point along the line, it will return back due to the restoring force that comes into the day. But if the charge is displaced slightly from the null – point along normal to the line it will not return. This is because the resultant force due to the configuration of two charges will take it away from the null point. For the test charge to be in stable equilibrium restoring force must come into play, when it is displaced in any direction. Hence the test charge cannot be in stable equilibrium.
Question 33.
A particle of mass m and charge (-q) enters the region between the two charged plates initially moving along x-axis with speed σx, (like particle 1 in figure.) The length of plate is L and a uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL2/(2m υx2).
Answer:
Consider a uniform electric field %20(4).png) set up between two oppositely charged parallel plates (Figure). Let a positively charged particle having charge +q and mass m enters the region of electric field E at O with velocity E along X-direction.
set up between two oppositely charged parallel plates (Figure). Let a positively charged particle having charge +q and mass m enters the region of electric field E at O with velocity E along X-direction.
Step 1.%20(4).png)
Force acting on the charge +q due to electric field E is given by
%20(1).png) =Q
=Q %20(4).png)
The direction of the force is along the direction of%20(2).png) and hence the charged particle is deflected accordingly.
and hence the charged particle is deflected accordingly.
Acceleration produced in the charged particle is given by
%20(3).png)
Step 2.
The charged particle will accelerate in the direction of E . As soon as the particle leaves the region of electric field, it travels due to inertia of motion and hits the screen at point P. Let t be the time taken by the charged particle to traverse the region of electric field of length L. Let y be the distance travelled by the particle along y-direction (i.e. direction of electric field). Using a standard equation of motion,
S = ut +.png)
For horizontal motion. S = L, u = υx and a = 0.
(∴ no force acts on the particle along x-direction)
From equation (ii), we have%20(2).png)
Equation (i) is the equation of a parabola.
Hence a charged particle moving in a uniform electric field follows a parabolic path.
Question 34.
Suppose that the particle in Q 1.33 is an electron projected with velocity
υx = 2.0 x 106 ms-1. If E between the plates separated by 0.5 cm is 9.1 x 102 N/C, where
will the electron strike the upper plate ? ( |e| = 1.6 x 10-19 C, me = 9.1 x 10-31 kg.)
Answer:%20(1).png)
NCERT Solutions for Class 12 Physics PDF
- Chapter 2 Electrostatic Potential and Capacitance
- Chapter 3 Current Electricity
- Chapter 4 Moving Charges and Magnetism
- Chapter 5 Magnetism and Matter
- Chapter 6 Electromagnetic Induction
- Chapter 7 Alternating Current
- Chapter 8 Electromagnetic Waves
- Chapter 9 Ray Optics and Optical Instruments
- Chapter 10 Wave Optics
- Chapter 11 Dual Nature of Radiation and Matter
- Chapter 12 Atoms
- Chapter 13 Nuclei
- Chapter 14 Electronics Devices
- Chapter 15 Communication Systems

%20(37).png)
%20(31).png)


