NCERT Solutions Class 12 Maths Chapter-8 (Application Of Integrals)Exercise 8.1
NCERT Solutions Class 12 Maths from class
12th Students will get the answers of
Chapter-8 (Application Of Integrals)Exercise 8.1 This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of
NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.
NCERT Question-Answer
Class 12 Mathematics
Chapter-8 (Application Of Integrals)
Questions and answers given in practice
Chapter-8 (Application Of Integrals)
Exercise 8.1
Q1. Find the area of the region bounded by the curve y2=x and the lines x = 1, x = 4 and the x-axis in the first quadrant.
Answer. 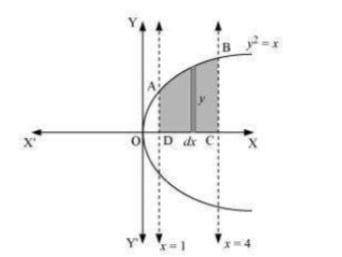 The area of the region bounded by the curve, y2 = x, the lines, x = 1 and x = 4, and the x-axis is the area ABCD. Area of ABCD=∫4ydx=∫√xdx=[3232]1 =23[(4)32−(1)32]=23[8−1]=143 units
The area of the region bounded by the curve, y2 = x, the lines, x = 1 and x = 4, and the x-axis is the area ABCD. Area of ABCD=∫4ydx=∫√xdx=[3232]1 =23[(4)32−(1)32]=23[8−1]=143 units
Q2. Find the area of the region bounded by y2=9x, x = 2, x = 4 and the x-axis in the first quadrant.
Answer. 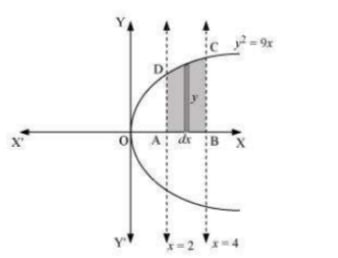 The area of the region bounded by the curve, y2 = 9x, x = 2, and x = 4, and the x-axis is the area ABCD. Area of ABCD=∫42ydx=∫423√xdx=3[32]42=2[x32]42 =2[(4)32−(2)32]=2[8−2√2]=(16−4√2) units
The area of the region bounded by the curve, y2 = 9x, x = 2, and x = 4, and the x-axis is the area ABCD. Area of ABCD=∫42ydx=∫423√xdx=3[32]42=2[x32]42 =2[(4)32−(2)32]=2[8−2√2]=(16−4√2) units Q3. Find the area of the region bounded by x2=4y, y = 2, y = 4 and the y-axis in the first quadrant.
Answer. 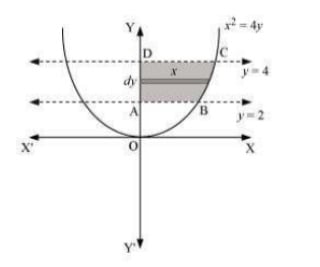 the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis is the area ABCD. Area of ABCD=∫42xdy=∫422√ydy=2∫42√ydy=2[322]2 =43[(4)32−(2)32]=43[8−2√2]=(32−8√23) units
the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis is the area ABCD. Area of ABCD=∫42xdy=∫422√ydy=2∫42√ydy=2[322]2 =43[(4)32−(2)32]=43[8−2√2]=(32−8√23) units
Q4. Find the area of the region bounded by the ellipse x216+y29=1
Answer. The given equation of the ellipse, x216+y29=1, can be represented as 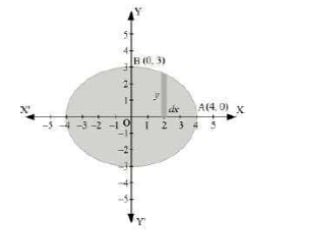 It can be observed that the ellipse is symmetrical about x-axis and y-axis. ∴ Area bounded by ellipse = 4 × Area of OAB Area of OAB=∫40ydx=∫40√1−x216dx=34∫40√16−x2dx =34[x2√16−x2+162sin−1x4]40=34[2√16−16+8sin−1(1)−0−8sin−1(0)]=34[8π2]=34[4π]=3π Therefore, area bounded by the ellipse = 4 × 3π = 12π units
It can be observed that the ellipse is symmetrical about x-axis and y-axis. ∴ Area bounded by ellipse = 4 × Area of OAB Area of OAB=∫40ydx=∫40√1−x216dx=34∫40√16−x2dx =34[x2√16−x2+162sin−1x4]40=34[2√16−16+8sin−1(1)−0−8sin−1(0)]=34[8π2]=34[4π]=3π Therefore, area bounded by the ellipse = 4 × 3π = 12π units
Q5. Find the area of the region bounded by the ellipse x24+y29=1
Answer. The given equation of the ellipse can be represented as 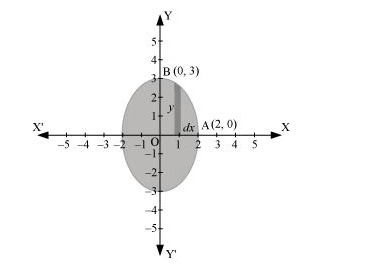 x24+y29=1⇒y=3√1−x24 It can be observed that the ellipse is symmetrical about x-axis and y-axis. ∴ Area bounded by ellipse = 4 × Area OAB ∴ Area of OAB =∫20ydx=∫203√1−x24dx[ Using (1)]=32∫20√4−x2dx =32[x2√4−x2+42sin−x2]20=32[2π2]=3π2 Therefore, area bounded by the ellipse =4×3π2=6π units
x24+y29=1⇒y=3√1−x24 It can be observed that the ellipse is symmetrical about x-axis and y-axis. ∴ Area bounded by ellipse = 4 × Area OAB ∴ Area of OAB =∫20ydx=∫203√1−x24dx[ Using (1)]=32∫20√4−x2dx =32[x2√4−x2+42sin−x2]20=32[2π2]=3π2 Therefore, area bounded by the ellipse =4×3π2=6π units
Q6. Find the area of the region in the first quadrant enclosed by x-axis, line x=√3y and the circle x2+y2=4
Answer. The area of the region bounded by the circle,x2+y2=4,x=√3y , and the x-axis is the area OAB.  The point of intersection of the line and the circle in the first quadrant is (√3,1) . Area OAB = Area ΔOCA + Area ACB Area of OAC=12×OC×AC=12×√3×1=√32…(i) Area of ABC=∫2√3ydx =∫2√3√4−x2dx=[x2√4−x2+42sin−1x2]2√5=[2×π2−√32√4−3−2sin−1(√32)]=[π−√32−2(13)]=[π−√32−2π3]=[π3−√32]...(ii) Therefore, area enclosed by x -axis, the line x=√3y, and the circle x2+y2=4 in the first √3π2+3√22=π3 units
The point of intersection of the line and the circle in the first quadrant is (√3,1) . Area OAB = Area ΔOCA + Area ACB Area of OAC=12×OC×AC=12×√3×1=√32…(i) Area of ABC=∫2√3ydx =∫2√3√4−x2dx=[x2√4−x2+42sin−1x2]2√5=[2×π2−√32√4−3−2sin−1(√32)]=[π−√32−2(13)]=[π−√32−2π3]=[π3−√32]...(ii) Therefore, area enclosed by x -axis, the line x=√3y, and the circle x2+y2=4 in the first √3π2+3√22=π3 units
Q7. Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2
Answer. The area of the smaller part of the circle, x2+y2=a2, cut off by the line, area ABCDA. 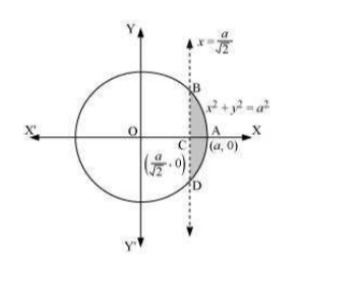 It can be observed that the area ABCD is symmetrical about x-axis. ∴ Area ABCD = 2 × Area ABC Area of ABC=∫πaydx=∫π√2√a2−x2dx=[x2√a2−x2+a22sin−1xa]aa√2=[a22(π2)−a2√2√a2−a22−a22sin−1(1√2)] =a2π4−a2√2⋅a√2−a22(π4)=a2π4−a24−a2π8=a24[π−1−π2]=a24[π2−1]⇒Area ABCD=2[a22(π2−1)]=a22(π2−1) Therefore, the area of smaller part of the circle, x2+y2=a2, cut off by the line, x=a√2a22(π2−1) units.
It can be observed that the area ABCD is symmetrical about x-axis. ∴ Area ABCD = 2 × Area ABC Area of ABC=∫πaydx=∫π√2√a2−x2dx=[x2√a2−x2+a22sin−1xa]aa√2=[a22(π2)−a2√2√a2−a22−a22sin−1(1√2)] =a2π4−a2√2⋅a√2−a22(π4)=a2π4−a24−a2π8=a24[π−1−π2]=a24[π2−1]⇒Area ABCD=2[a22(π2−1)]=a22(π2−1) Therefore, the area of smaller part of the circle, x2+y2=a2, cut off by the line, x=a√2a22(π2−1) units.
Q8. The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Answer.

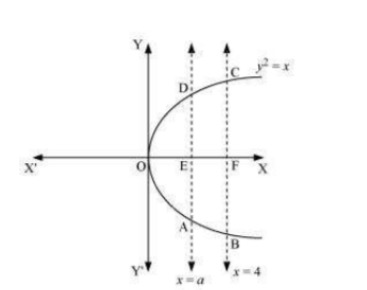 It can be observed that the area ABCD is symmetrical about x-axis. ∴ Area ABCD = 2 × Area ABC Area OED=Area EFCD Area OED=∫t0ydx=∫π0√xdx=[32]a0=23(a)32 ...(i) Area of EFCD=∫40√xdx=[3232]0=23[8−a32] …(ii) From (1) and (2), we obtain 23(a)32=23[8−(a)32]⇒2⋅(a)32=8⇒(a)32=4⇒a=(4)23 Therefore, the value of a is (4)23
It can be observed that the area ABCD is symmetrical about x-axis. ∴ Area ABCD = 2 × Area ABC Area OED=Area EFCD Area OED=∫t0ydx=∫π0√xdx=[32]a0=23(a)32 ...(i) Area of EFCD=∫40√xdx=[3232]0=23[8−a32] …(ii) From (1) and (2), we obtain 23(a)32=23[8−(a)32]⇒2⋅(a)32=8⇒(a)32=4⇒a=(4)23 Therefore, the value of a is (4)23Q9. Find the area of the region bounded by the parabola y = x2 and y=|x|
Answer. The area bounded by the parabola, x2=y, and the line, y=|x|, can be represented as 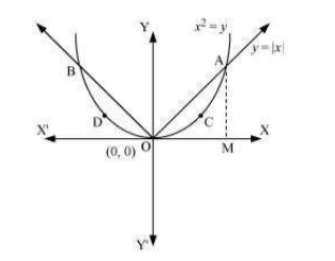 The given area is symmetrical about y -axis. ∴ Area OACO = Area ODBO The point of intersection of parabola, x2=y, and line, y=x, is A (1,1) . Area of OACO= Area ΔOAB− Area OBACO ∴ Area of ΔOAB=12×OB×AB=12×1×1=12 Area of OBACO =∫0ydx=∫x2dx=[x33]10=13⇒ Area of OACO = Area of ΔOAB− Area of OBACO =12−13=16Therefore,required area =2[16]=13
The given area is symmetrical about y -axis. ∴ Area OACO = Area ODBO The point of intersection of parabola, x2=y, and line, y=x, is A (1,1) . Area of OACO= Area ΔOAB− Area OBACO ∴ Area of ΔOAB=12×OB×AB=12×1×1=12 Area of OBACO =∫0ydx=∫x2dx=[x33]10=13⇒ Area of OACO = Area of ΔOAB− Area of OBACO =12−13=16Therefore,required area =2[16]=13
Q10. Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
Answer.
The area bounded by the curve, x2=4y, and line, x=4y−2, is represented by the shaded area OBAO. 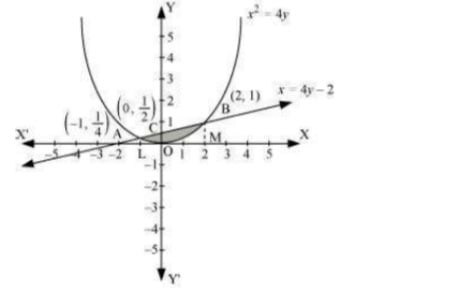 Let A and B be the points of intersection of the line and parabola. A are (−1,14) Coordinates of point Coordinates of point B are (2,1) We draw AL and BM perpendicular to x -axis. It can be observed that, Area OBAO= Area OBCO + Area OACO … (i) Then, Area OBCO= Area OMBC - Area OMBO =∫20x+24dx−∫20x24dx=14[x22+2x]20−14[x33]20 =14[2+4]−14[83]=32−23=56 Similarly, Area OACO = Area OLAC - Area OLAO =∫∞−1x+24dx−∫−1x24dx=14[x22+2x]0−1−14[x33]0=−14[(−1)22+2(−1)]−[−14((−1)33)]=−14[12−2]−112=12−18−112=724 Therefore, required area =(56+724)=98
Let A and B be the points of intersection of the line and parabola. A are (−1,14) Coordinates of point Coordinates of point B are (2,1) We draw AL and BM perpendicular to x -axis. It can be observed that, Area OBAO= Area OBCO + Area OACO … (i) Then, Area OBCO= Area OMBC - Area OMBO =∫20x+24dx−∫20x24dx=14[x22+2x]20−14[x33]20 =14[2+4]−14[83]=32−23=56 Similarly, Area OACO = Area OLAC - Area OLAO =∫∞−1x+24dx−∫−1x24dx=14[x22+2x]0−1−14[x33]0=−14[(−1)22+2(−1)]−[−14((−1)33)]=−14[12−2]−112=12−18−112=724 Therefore, required area =(56+724)=98Q11. Find the area of the region bounded by the curve y2 = 4x and the line x = 3
Answer. The region bounded by the parabola, y2=4x, and the line, x=3, is the area OACO. 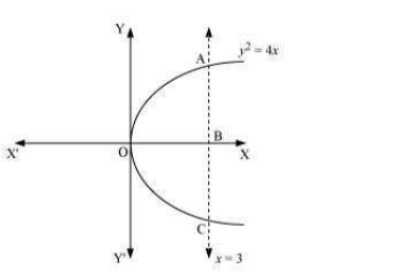 The area OACO is symmetrical about x -axis. ∴ Area of OACO=2 (Area of OAB) Area OACO =2[∫30ydx]=2∫2√xdx=4[x32]30=83[(3)32]=8√3 Therefore,the reqiured area is 8√3Q12. Area lying in the first quadrant and bounded by the circle x2+y2 = 4 and the lines x = 0 and x = 2 is A. π B. π2 C. π3 D. π4
The area OACO is symmetrical about x -axis. ∴ Area of OACO=2 (Area of OAB) Area OACO =2[∫30ydx]=2∫2√xdx=4[x32]30=83[(3)32]=8√3 Therefore,the reqiured area is 8√3Q12. Area lying in the first quadrant and bounded by the circle x2+y2 = 4 and the lines x = 0 and x = 2 is A. π B. π2 C. π3 D. π4
Answer. The area bounded by the circle and the lines, x=0 and x=2, in the first quadrant is represented as 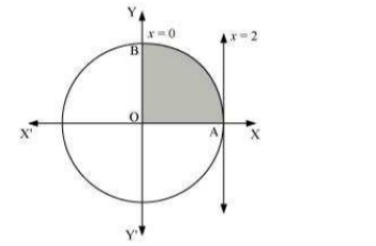 ∴ Area OAB=∫20ydx=∫20√4−x2dx=[x2√4−x2+42sin−1x2]20=2(π2)=π units Thus,the correct answer is A.
∴ Area OAB=∫20ydx=∫20√4−x2dx=[x2√4−x2+42sin−1x2]20=2(π2)=π units Thus,the correct answer is A.
Q13. Area of the region bounded by the curve y2=4x,y-axis and the line y = 3 is A. 2 B. 94 C. 93 D. 92
Answer. The bounded by the curve, y2=4x,y -axis, and y=3 is represented as 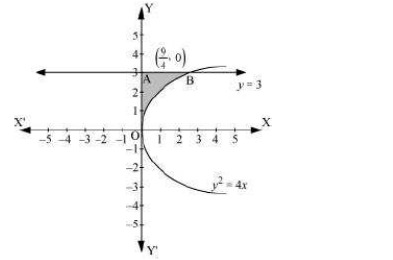 ∴ Area OAB=∫30xdy=∫30y24dy=14[y33]30=112(27)=94 units Thus the correct answer is B.
∴ Area OAB=∫30xdy=∫30y24dy=14[y33]30=112(27)=94 units Thus the correct answer is B.
Chapter-8 (integrals)
 The area of the region bounded by the curve, = x, the lines, x = 1 and x = 4, and the x-axis is the area ABCD.
The area of the region bounded by the curve, = x, the lines, x = 1 and x = 4, and the x-axis is the area ABCD.  The area of the region bounded by the curve, = 9x, x = 2, and x = 4, and the x-axis is the area ABCD.
The area of the region bounded by the curve, = 9x, x = 2, and x = 4, and the x-axis is the area ABCD.  the area of the region bounded by = 4y, y = 2, y = 4 and the y-axis is the area ABCD.
the area of the region bounded by = 4y, y = 2, y = 4 and the y-axis is the area ABCD.  It can be observed that the ellipse is symmetrical about x-axis and y-axis. ∴ Area bounded by ellipse = 4 × Area of OAB Therefore, area bounded by the ellipse = 4 × 3π = 12π units
It can be observed that the ellipse is symmetrical about x-axis and y-axis. ∴ Area bounded by ellipse = 4 × Area of OAB Therefore, area bounded by the ellipse = 4 × 3π = 12π units It can be observed that the ellipse is symmetrical about x-axis and y-axis. ∴ Area bounded by ellipse = 4 × Area OAB
It can be observed that the ellipse is symmetrical about x-axis and y-axis. ∴ Area bounded by ellipse = 4 × Area OAB  The point of intersection of the line and the circle in the first quadrant is . Area OAB = Area ΔOCA + Area ACB
The point of intersection of the line and the circle in the first quadrant is . Area OAB = Area ΔOCA + Area ACB  It can be observed that the area ABCD is symmetrical about x-axis. ∴ Area ABCD = 2 × Area ABC
It can be observed that the area ABCD is symmetrical about x-axis. ∴ Area ABCD = 2 × Area ABC 
 It can be observed that the area ABCD is symmetrical about x-axis. ∴ Area ABCD = 2 × Area ABC Area OED=Area EFCD
It can be observed that the area ABCD is symmetrical about x-axis. ∴ Area ABCD = 2 × Area ABC Area OED=Area EFCD  Therefore,required area
Therefore,required area  Therefore, required area
Therefore, required area  Therefore,the reqiured area is
Therefore,the reqiured area is  Thus,the correct answer is A.
Thus,the correct answer is A. Thus the correct answer is B.
Thus the correct answer is B.









