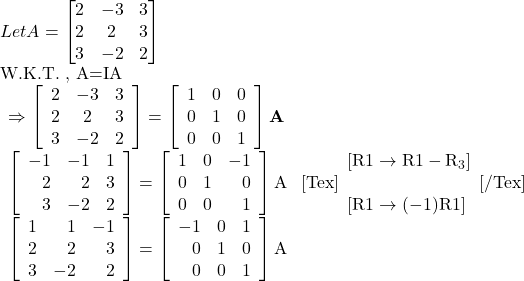NCERT Solutions Class 12 maths Chapter-3 (matrices)Exercise 3.4

NCERT Solutions Class 12 Maths from class 12th Students will get the answers of Chapter-3 (matrices)Exercise 3.4 This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.

Exercise 3.4  

Set 1

Using elementary transformations, find the inverse of each of the matrices, if it exists in Exercises 1 to 6.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Using elementary transformation, find the inverse of each of the matrices, if it exists in Exercises 7 to 14.

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Exercise 3.4 

Set 2

Question 11. 

Solution:

Question 12. 

Solution:

Here, both the elements of R2 of L.H.S. are 0.

Therefore, A-1 does not exist.

Question 13. 

Solution:

Question 14. 

Solution:

Here, both the elements of R2 of L.H.S. are 0.

Therefore, A-1 does not exist.

Question 15. 

Solution:

Therefore, A-1 =

Question 16. 

Solution:

Let A=

W.K.T. , A=IA

Question 17. 

Solution:

Let A=

W.K.T. , A=IA

Question 18. Matrices A and B will be inverse of each other only if:

(A) AB = BA  

(B) AB = BA = 0

(C) AB = 0, BA = I

(D) AB = BA = I

Solution:

According to the definition of inverse of square matrix,

Option (D) is correct

 i.e. AB=BA=I

Chapter-3 (matrices)

• Exercise 3.1
• Exercise 3.2
• Exercise 3.3