NCERT Solutions Class 12 Maths Chapter-13 (Probability)Exercise 13.4
NCERT Solutions Class 12 Maths from class
12th Students will get the answers of
Chapter-13 (Probability)Exercise 13.4 This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of
NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.
Exercise 13.4
Q1. State which of the following are not the probability distributions of a random variable. Give reasons for your answer. 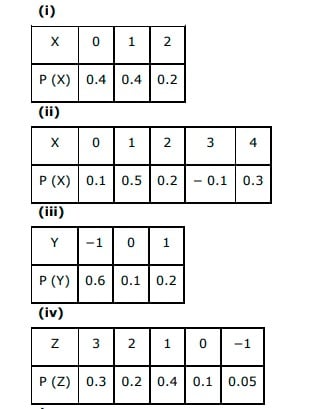
Answer. It is known that the sum of all the probabilities in a probability distribution is one. (i) Sum of the probabilities = 0.4 + 0.4 + 0.2 = 1 Therefore, the given table is a probability distribution of random variables. (ii) It can be seen that for X = 3, P (X) = −0.1 It is known that probability of any observation is not negative. Therefore, the given table is not a probability distribution of random variables. (iii) Sum of the probabilities = 0.6 + 0.1 + 0.2 = 0.9 ≠ 1 Therefore, the given table is not a probability distribution of random variables. (iv) Sum of the probabilities = 0.3 + 0.2 + 0.4 + 0.1 + 0.05 = 1.05 ≠ 1 Therefore, the given table is not a probability distribution of random variables.
Q2. An urn contains 5 red and 2 black balls. Two balls are randomly drawn. Let X represent the number of black balls. What are the possible values of X? Is X a random variable ?
Answer. The two balls selected can be represented as BB, BR, RB, RR, where B represents a black ball and R represents a red ball. X represents the number of black balls. ∴X (BB) = 2 X (BR) = 1 X (RB) = 1 X (RR) = 0 Therefore, the possible values of X are 0, 1, and 2. Yes, X is a random variable.
Q3. Let X represent the difference between the number of heads and the number of tails obtained when a coin is tossed 6 times. What are possible values of X?
Answer. A coin is tossed six times and X represents the difference between the number of heads and the number of tails. ∴X(6H,0T)=|6−0|=6x(5H,1T)=|5−1|=4 x(4H,2T)X(3H,3T)=|3−3|=0 X(2H,4T)=|2−4|=2X(1H,5T)=|1−5|=4X(0H,6T)=|0−6|=6 Thus, the possible values of X are 6, 4, 2, and 0.
Q4. Find the probability distribution of (i) number of heads in two tosses of a coin. (ii) number of tails in the simultaneous tosses of three coins. (iii) number of heads in four tosses of a coin.
Answer. (i) When one coin is tossed twice, the sample space is {HH, HT, TH, TT} Let X represent the number of heads. ∴ X (HH) = 2, X (HT) = 1, X (TH) = 1, X (TT) = 0 Therefore, X can take the value of 0, 1, or 2. It is known that, P(HH)=P(HT)=P(TH)=P(TT)=14 P (X = 0) = P (TT) = 14 P (X = 1) = P (HT) + P (TH) = 14+14=12 P(x=2)=P(HH)=14 Thus, the required probability distribution is as follows. 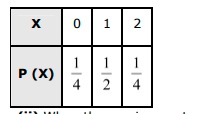 (ii) When three coins are tossed simultaneously, the sample space is Let X represent the number of tails. It can be seen that X can take the value of 0, 1, 2, or 3. P (X = 0) = P (HHH) = 18 P (X = 1) = P (HHT) + P (HTH) + P (THH) = 18+18+18=38 P (X = 2) = P (HTT) + P (THT) + P (TTH) = 18+18+18=38 P (X = 3) = P (TTT) = 18 Thus, the probability distribution is as follows.
(ii) When three coins are tossed simultaneously, the sample space is Let X represent the number of tails. It can be seen that X can take the value of 0, 1, 2, or 3. P (X = 0) = P (HHH) = 18 P (X = 1) = P (HHT) + P (HTH) + P (THH) = 18+18+18=38 P (X = 2) = P (HTT) + P (THT) + P (TTH) = 18+18+18=38 P (X = 3) = P (TTT) = 18 Thus, the probability distribution is as follows. 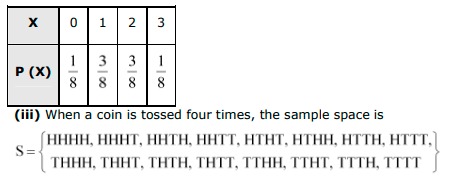 Let X be the random variable, which represents the number of heads. It can be seen that X can take the value of 0, 1, 2, 3, or 4. P(X=0)=P(TΠT)=116 P (X = 1) = P (TTTH) + P (TTHT) + P (THTT) + P (HTTT) =116+116+116+116=416=14 P (X = 2) = P (HHTT) + P (THHT) + P (TTHH) + P (HTTH) + P (HTHT) + P (THTH) =116+116+116+116+116+116=616=38P(x=3)=P(HHHT)+P(HHTH)+P(HTHH)P(THHH) =116+116+116+116=416=14P(x=4)=P(HHHH)=116 Thus, the probability distribution is as follows.
Let X be the random variable, which represents the number of heads. It can be seen that X can take the value of 0, 1, 2, 3, or 4. P(X=0)=P(TΠT)=116 P (X = 1) = P (TTTH) + P (TTHT) + P (THTT) + P (HTTT) =116+116+116+116=416=14 P (X = 2) = P (HHTT) + P (THHT) + P (TTHH) + P (HTTH) + P (HTHT) + P (THTH) =116+116+116+116+116+116=616=38P(x=3)=P(HHHT)+P(HHTH)+P(HTHH)P(THHH) =116+116+116+116=416=14P(x=4)=P(HHHH)=116 Thus, the probability distribution is as follows. 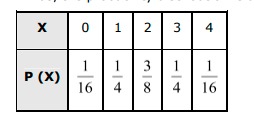
Q5. Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as (i) number greater than 4 (ii) six appears on at least one die
Answer. When a die is tossed two times, we obtain (6 × 6) = 36 number of observations. Let X be the random variable, which represents the number of successes. i. Here, success refers to the number greater than 4. P (X = 0) = P (number less than or equal to 4 on both the tosses) =46×46=49 P (X = 1) = P (number less than or equal to 4 on first toss and greater than 4 on second toss) + P (number greater than 4 on first toss and less than or equal to 4 on second toss) =46×26+46×26=49P(x=2)=P( number greater than 4 on both the tosses) =26×26=19 Thus, the probability distribution is as follows. 
Q6. From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.
Answer. It is given that out of 30 bulbs, 6 are defective. ⇒ Number of non-defective bulbs = 30 − 6 = 24 4 bulbs are drawn from the lot with replacement. Let X be the random variable that denotes the number of defective bulbs in the selected bulbs. P (X = 0) = P (4 non-defective and 0 defective) =4C0⋅45⋅45⋅4545=256625 P (X = 1) = P (3 non-defective and 1 defective) =4C1⋅(15)⋅(45)3=256625 P (X = 2) = P (2 non-defective and 2 defective) =4C2⋅(15)2⋅(45)2=96625 P (X = 3) = P (1 non-defective and 3 defective) =4C3⋅(15)3⋅(45)=16625 P (X = 4) = P (0 non-defective and 4 defective) =4C4⋅(15)4⋅(45)0=1625 Therefore, the required probability distribution is as follows. 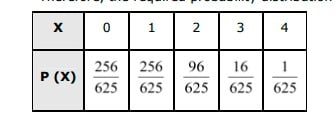
Q7. A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails.
Answer. Let the probability of getting a tail in the biased coin be x. ∴ P (T) = x ⇒ P (H) = 3x For a biased coin, P (T) + P (H) = 1 ⇒x+3x=1⇒4x=1⇒x=14∴P(T)=14 and P(H)=34 When the coin is tossed twice, the sample space is {HH, TT, HT, TH}. Let X be the random variable representing the number of tails. ∴ P (X = 0) = P (no tail) = P (H) × P (H) =34×34=916 P (X = 1) = P (one tail) = P (HT) + P (TH) =34⋅14+14⋅34=316+316=38 P(x=2)=P( two tails )=14×14=116 Therefore, the required probability distribution is as follows. 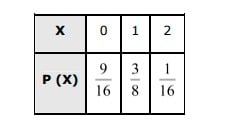
Q8. A random variable X has the following probability distribution: 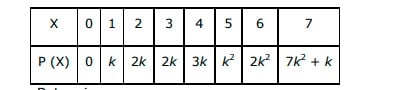 Determine (i) k (ii) P (X < 3) (iii) P (X > 6) (iv) P (0 < X < 3)
Determine (i) k (ii) P (X < 3) (iii) P (X > 6) (iv) P (0 < X < 3)
Answer. (i) It is known that the sum of probabilities of a probability distribution of random variables is one. ∴0+k+2k+2k+3k+k2+2k2+(7k2+k)=1⇒10k2+9k−1=0⇒(10k−1)(k+1)=0⇒k=−1,110k=−1 is not possible as the probability of an event is never negative. k=110 (ii) P (X < 3) = P (X = 0) + P (X = 1) + P (X = 2) =0+k+2k=3k=3×110=310 (iii)P(x>6)=P(x=7)=7k2+k=7×(110)2+110=7100+110=17100 ( iv) P(0<x<3)=P(x=1)+P(x=2)=k+2k=3k=3×110=310
Q9. The random variable X has a probability distribution P(X) of the following form, where k is some number: P(X)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩k, if x=02k, if x=13k, if x=20, otherwise (a) Determine the value of k. (b) Find P (X < 2), P (X ≤ 2), P(X ≥ 2)
Answer. (a) It is known that the sum of probabilities of a probability distribution of random variables is one. ∴ k + 2k + 3k + 0 = 1 ⇒ 6k = 1 ⇒k=16 (b) P(X<2)=P(X=0)+P(X=1)=k+2k=3k=36=12 P(X≤2)=P(X=0)+P(X=1)+P(X=2)=k+2k+3k=6k=66=1 P(X≥2)=P(X=2)+P(X>2)=3k+0=3k=36=12
Q10. Find the mean number of heads in three tosses of a fair coin.
Answer. Let X denote the success of getting heads. Therefore, the sample space is S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT} It can be seen that X can take the value of 0, 1, 2, or 3. ∴P(X=0)=P(TTT)=P(T)⋅P(T)⋅P(T)=12×12×12=18 ∴ P (X = 1) = P (HHT) + P (HTH) + P (THH) =12×12×12+12×12×12+12×12×12=38∴P(x=2)=P(HHT)+P(HTH)+P(THH) =12×12×12+12×12×12+12×12×12=38∴P(X=3)=P(HHH)∴P(X=3)=12×12×12=18 Therefore, the required probability distribution is as follows. 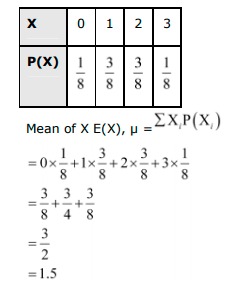
Q11. Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X.
Answer. Here, X represents the number of sixes obtained when two dice are thrown simultaneously. Therefore, X can take the value of 0, 1, or 2. ∴P(X=0)=P( not getting six on any of the dice )=2536 P (X = 1) = P (six on first die and no six on second die) + P (no six on first die and six on second die) =2(16×56)=1036 P(x=2)=P( six on both the dice )=136  =0×2536+1×1036+2×136=13
=0×2536+1×1036+2×136=13 Q12. Two numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers obtained. Find E(X).
Answer. The two positive integers can be selected from the first six positive integers without replacement in 6 × 5 = 30 ways X represents the larger of the two numbers obtained. Therefore, X can take the value of 2, 3, 4, 5, or 6. For X = 2, the possible observations are (1, 2) and (2, 1) ∴P(X=2)=230=115 For x=3, the possible observations are (1,3),(2,3),(3,1), and (3,2)∴P(X=3)=430=215 For X = 4, the possible observations are (1, 4), (2, 4), (3, 4), (4, 3), (4, 2), and (4, 1). ∴P(X=4)=630=15 For X = 5, the possible observations are (1, 5), (2, 5), (3, 5), (4, 5), (5, 4), (5, 3), (5, 2), and (5, 1). ∴P(X=5)=830=415 For X = 6, the possible observations are (1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 4), (6, 3), (6, 2), and (6, 1). ∴P(X=6)=1030=13 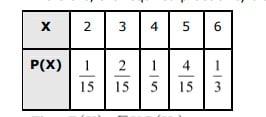 Then E(X)=∑XiP(Xi)=2⋅115+3⋅215+4⋅15+5⋅415+6⋅13=215+25+45+43+2=7015=143
Then E(X)=∑XiP(Xi)=2⋅115+3⋅215+4⋅15+5⋅415+6⋅13=215+25+45+43+2=7015=143
Q13. Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X.
Answer. When two fair dice are rolled, 6 × 6 = 36 observations are obtained. P(X=2)=P(1,1)=136 P(x=3)=P(1,2)+P(2,1)=236=118P(x=4)=P(1,3)+P(2,2)+P(3,1)=336=112P(x=5)=P(1,4)+P(2,3)+P(3,2)+P(4,1)=436=19P(x=6)=P(1,5)+P(2,4)+P(3,3)+P(4,2)+P(5,1)=536 P(x=7)=P(1,6)+P(2,5)+P(3,4)+P(4,3)+P(5,2)+P(6,1)=636=16P(x=8)=P(2,6)+P(3,5)+P(4,4)+P(5,3)+P(6,2)=536 P(X=9)=P(3,6)+P(4,5)+P(5,4)+P(6,3)=36P(X=10)=P(4,6)+P(5,5)+P(6,4)=336=112 P(x=11)=P(5,6)+P(6,5)=236=118P(x=12)=P(6,6)=136 Therefore, the required probability distribution is as follows. 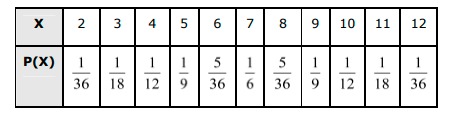 Then ,E(X)=∑Xi⋅P(Xi)=2×136+3×118+4×112+5×19+6×536+7×16+8×536+9×19+10×112+11×118+12×136=118+16+13+59+56+76+109+1+56+1118+13=7 E(X2)=ΣX2i⋅P(Xi)=4×136+9×118+16×112+25×19+36×536+49×16+64×536+81×19+100×112+121×118+144×136 =19+12+43+259+5+496+809+9+253+12118+4=98718=3296=54.833 Then ,var(X)=E(x2)−[E(X)]2=54.833−(7)2=54.833−49=5.833 ∴ Standard deviation =√Var(X)=√5.833=2.415
Then ,E(X)=∑Xi⋅P(Xi)=2×136+3×118+4×112+5×19+6×536+7×16+8×536+9×19+10×112+11×118+12×136=118+16+13+59+56+76+109+1+56+1118+13=7 E(X2)=ΣX2i⋅P(Xi)=4×136+9×118+16×112+25×19+36×536+49×16+64×536+81×19+100×112+121×118+144×136 =19+12+43+259+5+496+809+9+253+12118+4=98718=3296=54.833 Then ,var(X)=E(x2)−[E(X)]2=54.833−(7)2=54.833−49=5.833 ∴ Standard deviation =√Var(X)=√5.833=2.415 Q14. A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years. One student is selected in such a manner that each has the same chance of being chosen and the age X of the selected student is recorded. What is the probability distribution of the random variable X? Find mean, variance and standard deviation of X.
Answer. There are 15 students in the class. Each student has the same chance to be chosen. Therefore, the probability of each student to be selected is 1/15. The given information can be compiled in the frequency table as follows. 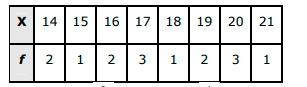 P(x=14)=215,P(x=15)=115,P(x=16)=215,P(x=16)=315 P(x=18)=115,P(x=19)=215,P(x=20)=315,P(x=21)=115 Therefore, the probability distribution of random variable X is as follows.
P(x=14)=215,P(x=15)=115,P(x=16)=215,P(x=16)=315 P(x=18)=115,P(x=19)=215,P(x=20)=315,P(x=21)=115 Therefore, the probability distribution of random variable X is as follows. 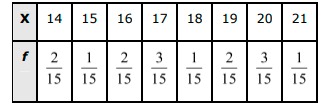 Then, mean of X = E(X) =∑XiP(Xi)=14×215+15×115+16×215+17×315+18×115+19×215+20×315+21×115 =115(28+15+32+51+18+38+60+21)=26315=17.53E(X2)=∑X2iP(Xi) =(14)2⋅215+(15)2⋅115+(16)2⋅215+(17)2⋅315+(18)2⋅115+(19)2⋅215+(20)2⋅315+(21)2⋅115=115⋅(392+225+512+867+324+722+1200+441)=468315=312.2 ∴ Variance (X)=E(X2)−[E(X)]2=312.2−(26315)2=312.2−307.4177=4.7823≈4.78 Standard derivation =√Variance(X)=√4.78=2.186≈2.19
Then, mean of X = E(X) =∑XiP(Xi)=14×215+15×115+16×215+17×315+18×115+19×215+20×315+21×115 =115(28+15+32+51+18+38+60+21)=26315=17.53E(X2)=∑X2iP(Xi) =(14)2⋅215+(15)2⋅115+(16)2⋅215+(17)2⋅315+(18)2⋅115+(19)2⋅215+(20)2⋅315+(21)2⋅115=115⋅(392+225+512+867+324+722+1200+441)=468315=312.2 ∴ Variance (X)=E(X2)−[E(X)]2=312.2−(26315)2=312.2−307.4177=4.7823≈4.78 Standard derivation =√Variance(X)=√4.78=2.186≈2.19 Q15. In a meeting, 70% of the members favour and 30% oppose a certain proposal. A member is selected at random and we take X = 0 if he opposed, and X = 1 if he is in favour. Find E(X) and Var (X). Choose the correct answer in each of the following:
Answer. It is given that P(x=0)=30%=30100=0.3P(X=1)=70%=70100=0.7 Therefore, the probability distribution is as follows. 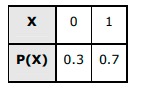 Then ,E(X)=∑XiP(Xi)=0×0.3+1×0.7=0.7E(X2)=∑X2iP(Xi)=02×0.3+(1)2×0.7=0.7 It is known that, var(x)=E(X2)−[E(X)]2=0.7−(0.7)2=0.7−0.49=0.21
Then ,E(X)=∑XiP(Xi)=0×0.3+1×0.7=0.7E(X2)=∑X2iP(Xi)=02×0.3+(1)2×0.7=0.7 It is known that, var(x)=E(X2)−[E(X)]2=0.7−(0.7)2=0.7−0.49=0.21 Q16. The mean of the numbers obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is (A) 1 (B) 2 (C) 5 (D) 83
Answer. Let X be the random variable representing a number on the die. The total number of observations is six. ∴P(X=1)=36=12P(X=2)=26=13P(X=5)=16 Therefore, the probability distribution is as follows.  =12×1+13×2+16⋅5=12+23+56=3+4+56=126=2 The correct answer is B.
=12×1+13×2+16⋅5=12+23+56=3+4+56=126=2 The correct answer is B.
Q17. Suppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. Then the value of E(X) is (A) 37221 (B) 513 (C) 113(D)213
Answer. Let X denote the number of aces obtained. Therefore, X can take any of the values of 0, 1, or 2. In a deck of 52 cards, 4 cards are aces. Therefore, there are 48 non-ace cards. ∴P(x=0)=P(0 ace and 2 non-ace cards )=4C0×48C23C2=11281326 P(x=1)=P(1 ace and 1 non-ace cards )=4C1×48C152C2=1921326 P(x=2)=P(2 ace and 0 non- ace cards )=4C2×48C052C2=61326 Thus, the probability distribution is as follows.  Then, E(X)=∑pixi=0×11281326+1×1921326+2×61326=2041326=213 Therefore, the correct answer is D.
Then, E(X)=∑pixi=0×11281326+1×1921326+2×61326=2041326=213 Therefore, the correct answer is D.
Chapter-13 (Probability)

 (ii) When three coins are tossed simultaneously, the sample space is Let X represent the number of tails. It can be seen that X can take the value of 0, 1, 2, or 3. P (X = 0) = P (HHH) = P (X = 1) = P (HHT) + P (HTH) + P (THH) = P (X = 2) = P (HTT) + P (THT) + P (TTH) = P (X = 3) = P (TTT) = Thus, the probability distribution is as follows.
(ii) When three coins are tossed simultaneously, the sample space is Let X represent the number of tails. It can be seen that X can take the value of 0, 1, 2, or 3. P (X = 0) = P (HHH) = P (X = 1) = P (HHT) + P (HTH) + P (THH) = P (X = 2) = P (HTT) + P (THT) + P (TTH) = P (X = 3) = P (TTT) = Thus, the probability distribution is as follows.  Let X be the random variable, which represents the number of heads. It can be seen that X can take the value of 0, 1, 2, 3, or 4. P (X = 1) = P (TTTH) + P (TTHT) + P (THTT) + P (HTTT) P (X = 2) = P (HHTT) + P (THHT) + P (TTHH) + P (HTTH) + P (HTHT) + P (THTH)
Let X be the random variable, which represents the number of heads. It can be seen that X can take the value of 0, 1, 2, 3, or 4. P (X = 1) = P (TTTH) + P (TTHT) + P (THTT) + P (HTTT) P (X = 2) = P (HHTT) + P (THHT) + P (TTHH) + P (HTTH) + P (HTHT) + P (THTH) 



 Determine (i) k (ii) P (X < 3) (iii) P (X > 6) (iv) P (0 < X < 3)
Determine (i) k (ii) P (X < 3) (iii) P (X > 6) (iv) P (0 < X < 3)



 Therefore, the probability distribution of random variable X is as follows.
Therefore, the probability distribution of random variable X is as follows.  Then, mean of X = E(X)
Then, mean of X = E(X) 












