NCERT Solutions Class 12 Maths Chapter-10 (Vector Algebra)Exercise 10.2
NCERT Solutions Class 12 Maths from class 12th Students will get the answers of Chapter-10 (Vector Algebra)Exercise 10.2 This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.
Exercise 10.2
Q1. Compute the magnitude of the following vectors: →a=^i+^j+^k;→b=2^i−7^j−3^k;→c=1√3^i+1√3^j−1√3^k
Answer. The given vectors are: →a=^i+^j+^k;→b=2^i−7^j−3^k;→c=1√3^i+1√3^j−1√3^k |→a|=√(1)2+(1)2+(1)2=√3|→b|=√(2)2+(−7)2+(−3)2=√4+49+9=√62 |→c|=
⎷(1√3)2+(1√3)2+(−1√3)2=√13+13+13=1
Q2. Write two different vectors having same magnitude.
Answer. Consider →a=(^i−2^j+3^k) and →b=(2^i+^j−3^k) It can be observed that |→a|=√12+(−2)2+32=√1+4+9=√14 and Consider a→=(i^−2j^+3k^) and b→=(2i^+j^−3k^) It can be observed that |a→|=12+(−2)2+32=1+4+9=14 and →b|=√22+12+(−3)2=√4+1+9=√14 Hence, →a and →b are two different vectors having the same magnitude. The vectors are different because they have different directions.
Q3. Write two different vectors having same direction.
Answer. Consider →p=(^i+^j+^k) and →q=(2^i+2^j+2^k) The direction cosines of →p are given by, Consider p→=(i^+j^+k^) and q→=(2i^+2j^+2k^) The direction cosines of p→ are given by, I=1√12+12+12=1√3,m=1√12+12+12=1√3, and n=1√12+12+12=1√3 The direction cosines of →q are given by l=2√22+22+22=22√3=1√3,m=2√22+22+22=22√3=1√3 and n=2√22+22+22=22√3=1√3 The direction cosines of →p and →q are the same. Hence, the two vectors have the same direction.
Q4. Find the values of x and y so that the vectors 2^i+3^j and x^i+y^y are equal.
Answer. The two vector 2^i+3^j and x^i+y^j will be equal if their corresponding components are equal. Hence, the required values of x and y are 2 and 3 respectively.
Q5. Find the scalar and vector components of the vector with initial point (2, 1) and terminal point( -5, 7).
Answer. The vector with the initial point p (2, 1) and terminal point Q ( 5, 7) can be given by, −−→PQ=(−5−2)^i+(7−1)^j⇒−−→PQ=−7^i+6^j Hence, the required scalar components are —7 and 6 while the vector components are −7^i and 6^j
Q6. Find the sum of the vectors →a=^i−2^j+˙k,→b=−2^i+4^j+5^k and →c=^i−6^j−7^k
Answer. The given vector are →a=^i−2^j+^k,→b=−2^i+4^j+5^k and →c=^i−6^j−7^k ∴→a+→b+→c=(1−2+1)^i+(−2+4−6)^j+(1+5−7)^k=0⋅^i−4^j−1⋅^k=−4^j−^k
Q7. Find the unit vector in the direction of the vector
Answer. The unit vector ^a in the direction of vector ¯¯¯a=^i+^j+2^k is given by ^a=→a|a||→a|=√12+12+22=√1+1+4=√6∴^a=→a|→a|=^i+^j+2^k√6=1√6^i+1√6^j+2√6˙k
Q8. Find the unit vector in the direction of vector →PQ , where p and Q are the points (1, 2, 3) and (4, S, 6), respectively.
Answer. The given points are P(1,2,3) and Q(4,5,6).∴−−→PQ=(4−1)^i+(5−2)^j+(6−3)^k=3^i+3^j+3^k|−−→PQ|=√32+32+32=√9+9+9=√27=3√3 Hence, the unit vector in the direction of ¯¯¯¯¯¯¯¯PQ is −−→PQ|−−→PQ|=3^i+3^j+3^k3√3=1√3^i+1√3^j+1√3˙k
Q9. For given vectors, ¯¯¯a=2^i−^ȷ+2^k and →b=−^i+^j−^k , find the unit vector in the direction of the vector →a+→b
Answer. The given vectors are →a=2^i−^j+2^k and →b=−^i+^j−^k→a=2^i−^j+2^k→b=−^i+^j−^k∴→a+→b=(2−1)^i+(−1+1)^j+(2−1)^k=1^i+0^j+1^k=^i+^k|→a+→b|=√12+12=√2 Hence, the unit vector in the direction of ¯¯¯a+→b) is (→a+→b)|→a+→b|=^i+^k√2=12^i+1√2^k
Q10. Find a vector in the direction of vector 5^i−^j+2^k which has magnitude 8 units.
Answer. Let →a=5^i−^j+2^k∴|→a|=√52+(−1)2+22=√25+1+4=√30∴^a=→a|→a|=5^i−^j+2^k√30 Hence, the vector in the direction of vector 5^i−^j+2^k which has magnitude 8 units is given by, 8^a=8(5^i−^j+2^k√30)=40√30^i−8√30^j+16√30^k=8(5→i−¯j+2→k√30) =40√30→i−8√30→j+16√30→k
Q11. Show that the vectors 2^i−3^j+4^k and −4^i+6^j−8^k are collinear.
Answer. Let →a=2^i−3^j+4^k and →b=−4^i+6^j−8^k It is observed that →b=−4^i+6^j−8^k=−2(2^i−3^j+4^k)=−2→a∴→b=λ→a where, λ=−2 Hence, the given vectors are collinear.
Q12. Find the direction cosines of the vector ^i+2^j+3^k
Answer. Let →a=^i+2^j+3^k∴|→a|=√12+22+32=√1+4+9=√14 Hence, the direction cosines of →a are (1√14,2√14,3√14)
Q13. Find the direction cosines of the vector joining the points A (I, 2, -3 ) and B (-1 , -2 , -3 ) directed from A to B.
Answer. The given points are A(1,2,−3) and B(−1,−2,1) . ∴−−→AB=(−1−1)^i+(−2−2)^j+{1−(−3)}^k⇒−−→AB=−2^i−4^j+4^k∴|−−→AB|=−√(−2)2+(−4)2+42=√4+16+16=√36=6 Hence, the direction cosines of `→a are (1√14,2√14,3√14)
Q14. Show that the vector ^i+^j+^k is equally inclined to the axes OX, OM, and OZ.
Answer. Let →a=^i+^j+^k Then, |→a|=√12+12+12=√3 Therefore, the dlrectlon coslnes of →aare(1√3,1√3,1√3) Then we have cosα=1√3,cosβ=1√3,cosγ=1√3 Hence, the given vector is equally inclined to axes OX, OM, and OZ.
Q15. Find the position vector of a point R which divides the line joining two points P and Q ^i+2^j−^k and −^i+^ȷ+^k whose position vectors are respectively, in the ratio 2:1 (i) internally (ii) externally
Answer. The position vector of point R dividing the line segment joining two points P and Q in the ratio m: n is given by: 1. Internally: m→b+n→am+n ii. Externally: m→b−n→am−n Position vectors of P and Q are given as: −−→OP=^i+2^j−^k and −−→OQ=−^i+^j+^k (i) The position vector Of point R Which divides the line joining two points p and Q internally in the ratio 2:1 is given by, ¯¯¯¯¯¯¯¯OR=2(−^i+^j+^k)+1(^i+2^j−^k)2+1=(−2^i+2^j+2^k)+(^i+2^j−^k)3=−^i+4^j+^k3=−13^i+43^j+13^k (ii) The position vector of point R which divides the line joining two points P and Q externally in the ratio 2:1 is given by, −−→OR=2(−^i+^j+˙k)−1(^i+2^j−˙k)2−1=(−2i+2^j+2^k)−(i+2^j−˙k)=−3i+3^k
Q16. Find the position vector of the midpoint of the vector joining the points P (2, 3, 4) and Q (4 , 1 , -2 )
Answer. The position vector of mid-point R of the vector joining points P (2, 3, 4) and Q (4, 1, - 2) is given by, −−→OR=(2^i+3^j+4^k)+(4^i+^j−2^k)2=(2+4)^i+(3+1)^j+(4−2)^k2=6^i+4^j+2^k2=3^i+2^j+^k
Q17. Show that the points A,B and C with position vectors, ¯¯¯a=3^i−4^j−4^k→b=2^i−^j+^k and →c=^i−3^j−5^k , respectively form the vertices of a right angled triangle.
Answer. position vectors Of points A, B, and c are respectively given as: →a=3^i−4^j−4^k,→b=2^i−^j+^k and →c=^i−3^j−5^k→a=3^i−4^j−4^k,→b=2^i−^j+^k and →c=^i−3^j−5^k ∴−−→AB=→b−→a=(2−3)^i+(−1+4)^j+(1+4)^k=−^i+3^j+5^k¯¯¯¯¯¯¯¯BC=→c−→b=(1−2)^i+(−3+1)^j+(−5−1)^k=−^i−2^j−6^k−−→CA=→a−→c=(3−1)^i+(−4+3)^j+(−4+5)^k=2^i−^j+^k ∴|−−→AB|2=(−1)2+32+52=1+9+25=35|BC|2=(−1)2+(−2)2+(−6)2=1+4+36=41|CA|2=22+(−1)2+12=4+1+1=6 ∴|−−→AB|2+|−−→CA|2=36+6=41=|−−→BC|2 Hence, ABC is a right-angled triangle.
Q18. In triangle ABC Which Of the following is not true: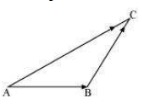 
A. ¯¯¯¯¯¯¯¯AB+−−→BC+−−→CA=¯¯¯0 B. ¯¯¯¯¯¯¯¯AB+−−→BC−−−→AC=→0 C. −−→AB+−−→BC−−−→CA=→0 D. ¯¯¯¯¯¯¯¯AB−−−→CB+−−→CA=→0
Answer. On applying the triangle law of addition in the given triangle, we have: −−→AB+−−→BC=−−→AC⇒−−→AB+BC=−CA⇒¯¯¯¯¯¯¯¯AB+−−→BC+¯¯¯¯¯¯¯¯CA=→0 ∴ The equation given in alternative A is true. −−→AB+−−→BC=−−→AC⇒−−→AB+−−→BC−−−→AC=→0∴ The equation given in altermative B is true. From equation (2), we have: Now, consider the equation given in altemative C: −−→AB+−−→BC−−−→CA=→0⇒−−→AB+−−→BC=¯¯¯¯¯¯¯¯CA −−→AC=−−→CA⇒−−→AC=−−−→AC⇒−−→AC+−−→AC=→0⇒2−−→AC=→0⇒−−→AC=→0 , which is not true. Hence, the equation given in altemative C is incorrect. The correct answer is C.
Q19. If →a and →b are two collinear vectors, then which of the following are incorrect: A. →b=λ→a , for some scalar λ B. →a=±→b C. the respective components of →a and →b are proportional D. both the vectors →a and →b have same direction, but different magnitudes
Answer. If →a and →b are two collinear vectors, then they are parallel. Therefore, we have: →b=λ→a (For some scalar λ) If λ=±1, then →a=±→b If →a=a1^i+a2^j+a3^k and →b=b1^i+b2^j+b3^k, then →b=λ→a. ⇒b1^i+b2^j+b3^k=λ(a1^i+a2^j+a3^k)⇒b1^i+b2^j+b3^k=(λa1)^i+(λa2)^j+(λa3)^k⇒b1=λa1,b2=λa2,b3=λa3⇒b1a1=b2a2=b3a3=λ Thus, the respective components of →a and →b are proportional. Thus, the respective components of →a and →b are proportional. However, vectors →a and →b can have different directions. Hence, the statement given in D is incorrect. The correct answer is D.
Chapter-10 (Vector Algebra)
