NCERT Solutions Class 12 Maths Chapter-10 (Vector Algebra)Exercise 10.1

NCERT Solutions Class 12 Maths from class 12th Students will get the answers of Chapter-10 (Vector Algebra)Exercise 10.1 This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.

NCERT Question-Answer

Class 12 Mathematics

Chapter-10 (Vector Algebra)

Questions and answers given in practice

Chapter-10 (Vector Algebra)

Exercise 10.1

Q1. Represent graphically a displacement of 40 km, ${30}^{\circ }$ east of north.

Answer. 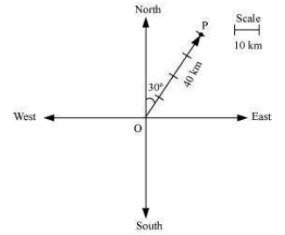 Here vector $\overrightarrow{OP}$ represent the displacement of 40 km, ${30}^{\circ }$ East of north .

Q2. Classify the following measures as scalars and vectors. (i) $10kg\text{(ii)}2\text{metres north-west (iii)}{40}^{\circ }$ (iv) $40\text{watt}\left(v\right){10}^{-19}\text{coulomb (vi)}20m/s^2$

Answer. (i) 10 kg is a scalar quantity because it involves only magnitude. (ii) 2 meters north-west is a vector quantity as it involves both magnitude and direction. (iii) ${40}^{\circ }$ is a scalar quantity as it involves only magnitude. (iv) 40 watts is a scalar quantity as it involves only magnitude. (v) ${10}^{-19}$ coulomb is a scalar quantity as it involves only magnitude. (vi) $20m/s^2$ is a vector quantity as it involves magnitude as well as direction.

Q3. Classify the following as scalar and vector quantities. (i) time period (ii) distance (iii) force (iv) velocity (v) work done

Answer. (i) Time period is a scalar quantity as it involves only magnitude. (ii) Distance is a scalar quantity as it involves only magnitude. (iii) Force is a vector quantity as it involves both magnitude and direction. (iv) Velocity is a vector quantity as it involves both magnitude as well as direction. (v) Work done is a scalar quantity as it involves only magnitude.

Q4. In Figure, identify the following vectors. 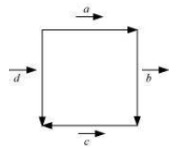 (i) Coinitial (ii) Equal (iii) Collinear but not equal

Answer. (i) Vectors $\overrightarrow{a}$ and $\overrightarrow{d}$ are coinitial because they have the same initial point. (ii) vectors $\overrightarrow{b}$ and $\overrightarrow{d}$ are equal because they have the same magnitude and direction. (iii) Vectors $\overrightarrow{a}$ and $\overrightarrow{c}$ are collinear but not equal. This is because although they are parallel, their directions are not the same.

Q5. Answer the following as true or false. (i) $\overrightarrow{a}$ and $\overrightarrow{-a}$ are collinear. (ii) Two collinear vectors are always equal in magnitude. (iii) Two vectors having same magnitude are collinear. (iv) Two collinear vectors having the same magnitude are equal.

Answer. (i) True. Vectors $\overrightarrow{a}$ and $\overrightarrow{-a}$ are parallel to the same line. (ii) False. Collinear vectors are those vectors that are parallel to the same line. (iii) False.

Chapter-10 (Vector Algebra)

• Exercise 10.2
• Exercise 10.3
• Exercise 10.4