NCERT Solutions Class 12 Maths (Probability) Miscellaneous Exercise

NCERT Solutions Class 12 Maths from class 12th Students will get the answers of Chapter-13 (Probability) Miscellaneous Exercise This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.

Q1. A and B are two events such that P (A) ≠ 0. Find P(B|A), if (i) A is a subset of B (ii) A ∩ B = φ

Answer. It is given that, P (A) ≠ 0 (i) A is a subset of B. $\begin{array}{c}\Rightarrow A\cap B=A\\ \therefore P(A\cap B)=P(B\cap A)=P\left(A\right)\\ \therefore P\left(B|A\right)=\frac{P(B\cap A)}{P\left(A\right)}=\frac{P\left(A\right)}{P\left(A\right)}=1\end{array}$ $\begin{array}{c}\text{(ii)}A\cap B=\varphi \\ \Rightarrow P(A\cap B)=0\\ \therefore P\left(B|A\right)=\frac{P(A\cap B)}{P\left(A\right)}=0\end{array}$

Q2. A couple has two children, (i) Find the probability that both children are males, if it is known that at least one of the children is male. (ii) Find the probability that both children are females, if it is known that the elder child is a female.

Answer. If a couple has two children, then the sample space is S = {(b, b), (b, g), (g, b), (g, g)} (i) Let E and F respectively denote the events that both children are males and at least one of the children is a male. $\begin{array}{c}\therefore E\cap F=\left\{\right(b,b\left)\right\}\Rightarrow P(E\cap F)=\frac{1}{4}\\ P\left(E\right)=\frac{1}{4}\\ P\left(F\right)=\frac{3}{4}\\ \Rightarrow P\left(EF\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3}\end{array}$ (ii) Let A and B respectively denote the events that both children are females and the elder child is a female.$A=\left\{\right(g,g\left)\right\}\Rightarrow P\left(A\right)=\frac{1}{4}B=\left\{\right(g,b),(g,g\left)\right\}\Rightarrow P\left(B\right)=\frac{2}{4}A\cap B=\left\{\right(g,g\left)\right\}\Rightarrow P(A\cap B)=\frac{1}{4}$$P\left(A|B\right)=\frac{P(A\cap B)}{P\left(B\right)}=\frac{\frac{1}{4}}{\frac{2}{4}}=\frac{1}{2}$

Q3. Suppose that 5% of men and 0.25% of women have grey hair. A grey haired person is selected at random. What is the probability of this person being male? Assume that there are equal number of males and females.

Answer. It is given that 5% of men and 0.25% of women have grey hair. Therefore, percentage of people with grey hair = (5 + 0.25) % = 5.25% Probability that the selected haired person is a male $=\frac{5}{5.25}=\frac{20}{21}$

Q4. Suppose that 90% of people are right-handed. What is the probability that at most 6 of a random sample of 10 people are right-handed?

Answer. A person can be either right-handed or left-handed. It is given that 90% of the people are right-handed. $\begin{array}{c}\therefore p=P\left(\text{right-handed}\right)=\frac{9}{10}\\ q=P\left(\text{left-handed}\right)=1-\frac{9}{10}=\frac{1}{10}\end{array}$ Using binomial distribution, the probability that more than 6 people are right-handed is given by, 

Q5. An urn contains 25 balls of which 10 balls bear a mark 'X' and the remaining 15 bear a mark 'Y'. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that (i) all will bear 'X' mark. (ii) not more than 2 will bear 'Y' mark. (iii) at least one ball will bear 'Y' mark. (iv) the number of balls with 'X' mark and 'Y' mark will be equal. 6. In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is 5

Answer. Total number of balls in the urn = 25 Balls bearing mark ‘X’ = 10 Balls bearing mark ‘Y’ = 15 $p=P\left({\text{ball bearing mark}}^{\prime }{X}^{\prime }\right)=\frac{10}{25}=\frac{2}{5}$ $q=P\left({\text{ball bearing mark}}^{\prime }{Y}^{\prime }\right)=\frac{15}{25}=\frac{3}{5}$ Six balls are drawn with replacement. Therefore, the number of trials are Bernoulli trials. Let Z be the random variable that represents the number of balls with ‘Y’ mark on them in the trials. $\begin{array}{c}\text{Clearly, Z has a binomial distribution with}n=6\text{and}p=\frac{2}{5}\\ P(Z=z){=}^n{C}_z{p}^{n-z}{q}^z\end{array}$ (i) P (all will bear ‘X’ mark) =$=P(Z=0){=}^{\circ }{C}_0{\left(\frac{2}{5}\right)}^6={\left(\frac{2}{5}\right)}^6$ (ii) P (not more than 2 bear ‘Y’ mark) = P (Z ≤ 2) $\begin{array}{c}{=}^6{C}_0\left(p{)}^6\right(q{)}^0{+}^6{C}_1\left(p{)}^5\right(q{)}^1{+}^6{C}_2\left(p{)}^4\right(q{)}^2\\ ={\left(\frac{2}{5}\right)}^6+6{\left(\frac{2}{5}\right)}^5\left(\frac{3}{5}\right)+15{\left(\frac{2}{5}\right)}^4{\left(\frac{3}{5}\right)}^2\\ ={\left(\frac{2}{5}\right)}^4[{\left(\frac{2}{5}\right)}^2+6\left(\frac{2}{5}\right)\left(\frac{3}{5}\right)+15{\left(\frac{3}{5}\right)}^2]\end{array}$ $\begin{array}{cc}& ={\left(\frac{2}{5}\right)}^4[\frac{4}{25}+\frac{36}{25}+\frac{135}{25}]\\ & ={\left(\frac{2}{5}\right)}^4\left[\frac{175}{25}\right]\\ & =7{\left(\frac{2}{5}\right)}^4\end{array}$ (iii) P (at least one ball bears ‘Y’ mark) = P (Z ≥ 1) = 1 − P (Z = 0) $=1-{\left(\frac{2}{5}\right)}^6$ (iv) P (equal number of balls with ‘X’ mark and ‘Y’ mark) = P (Z = 3) =$\begin{array}{c}{}^6{C}_3{\left(\frac{2}{54}\right)}^3{\left(\frac{3}{5}\right)}^3\\ =\frac{20\times 8\times 27}{15625}\\ =\frac{864}{3125}\end{array}$

Q6. What is the probability that he will knock down fewer than 2 hurdles? The probability that he will clear each hurdle is 5/6 . What is the probability that he will knock down fewer than 2 hurdles?

Answer. Let p and q respectively be the probabilities that the player will clear and knock down the hurdle.$\begin{array}{c}\therefore p=\frac{5}{6}\\ \Rightarrow q=1-p=1-\frac{5}{6}=\frac{1}{6}\end{array}$ Let X be the random variable that represents the number of times the player will knock down the hurdle. Therefore, by binomial distribution, we obtain $\begin{array}{c}P(X=x){=}^n{C}_x{p}^{n-x}{q}^x\\ P\left(\text{player knocking down less than}2\text{hurdles}\right)=P(x<2)\\ =P(X=0)+P(X=1)\\ {}^{10}{C}_0\left(q{)}^0\right(p{)}^{10}{+}^{10}{C}_1\left(q\right)(p{)}^9\end{array}$ $\begin{array}{cc}& ={\left(\frac{5}{6}\right)}^{10}+10\cdot \frac{1}{6}\cdot {\left(\frac{5}{6}\right)}^9\\ & ={\left(\frac{5}{6}\right)}^9[\frac{5}{6}+\frac{10}{6}]\\ & =\frac{5}{2}{\left(\frac{5}{6}\right)}^9\\ & =\frac{(5{)}^{10}}{2\times (6{)}^9}\end{array}$

Q7. A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the die.

Answer. The probability of getting a six in a throw of die is $\frac{1}{6}\text{and not getting a six is}6$ $\begin{array}{c}{\text{Let}}^{p=\frac{1}{6}\text{and}q=\frac{5}{6}}\\ \text{The probability that the}2\text{sixes come in the first five throws of the die is}\\ {}^5{C}_2{\left(\frac{1}{6}\right)}^2{\left(\frac{5}{6}\right)}^3=\frac{10\times (5{)}^5}{(6{)}^5}\end{array}$ Probability that third six comes in the sixth throw = $\frac{10\times (5{)}^3}{(6{)}^5}\times \frac{1}{6}$ $\begin{array}{cc}& =\frac{10\times 125}{(6{)}^6}\\ & =\frac{10\times 125}{46656}\\ & =\frac{625}{23328}\end{array}$

Q8. If a leap year is selected at random, what is the chance that it will contain 53 tuesdays?

Answer. In a leap year, there are 366 days i.e., 52 weeks and 2 days. In 52 weeks, there are 52 Tuesdays. Therefore, the probability that the leap year will contain 53 Tuesdays is equal to the probability that the remaining 2 days will be Tuesdays. The remaining 2 days can be Monday and Tuesday Tuesday and Wednesday Wednesday and Thursday Thursday and Friday Friday and Saturday Saturday and Sunday Sunday and Monday Total number of cases = 7 Favourable cases = 2 ∴Probability that a leap year will have 53 Tuesdays $=\frac{2}{7}$

Q9. An experiment succeeds twice as often as it fails. Find the probability that in the next six trials, there will be at least 4 successes.

Answer. The probability of success is twice the probability of failure. Let the probability of failure be x. ∴ Probability of success = 2x $\begin{array}{c}x+2x=1\\ \Rightarrow 3x=1\\ \Rightarrow x=\frac{1}{3}\\ \therefore 2x=\frac{2}{3}\end{array}$ $\begin{array}{c}\text{Let}p=\frac{1}{3}\text{and}q=\frac{2}{3}\\ \text{Let}X\text{be the random variable that represents the number of successes in six trials.}\\ \text{By binomial distribution, we obtain}\end{array}$ $\begin{array}{c}P(x=x){=}^n{C}_x{p}^{n-x}{q}^x\\ \text{Probability of at least}4\text{successes}=P(x\ge 4)\\ =P(x=4)+P(x=5)+P(x=6)\\ {=}^6{C}_4{\left(\frac{2}{3}\right)}^4{\left(\frac{1}{3}\right)}^2{+}^6{C}_5{\left(\frac{2}{3}\right)}^5\left(\frac{1}{3}\right){+}^6{C}_6{\left(\frac{2}{3}\right)}^6\end{array}$ $\begin{array}{cc}& =\frac{15(2{)}^4}{3^6}+\frac{6(2{)}^5}{3^6}+\frac{(2{)}^6}{3^6}\\ & =\frac{(2{)}^4}{(3{)}^6}[15+12+4]\\ & =\frac{31\times 2^4}{(3{)}^6}\\ & =\frac{31}{9}{\left(\frac{2}{3}\right)}^4\end{array}$

Q10. How many times must a man toss a fair coin so that the probability of having at least one head is more than 90%?

Answer. Let the man toss the coin n times. The n tosses are n Bernoulli trials. Probability (p) of getting a head at the toss of a coin ½ is . $\begin{array}{c}p=\frac{1}{2}q=\frac{1}{2}\\ \therefore P(X=x){=}^n{C}_x{p}^{a-x}{q}^x{=}^n{C}_x{\left(\frac{1}{2}\right)}^{n-x}{\left(\frac{1}{2}\right)}^x{=}^n{C}_x{\left(\frac{1}{2}\right)}^n\end{array}$ It is given that, $\begin{array}{c}P\left(\text{getting at least one head}\right)>\frac{90}{100}\\ P(x\ge 1)>0.9\\ 1-P(x=0)>0.9\\ 1{-}^n{C}_0\cdot \frac{1}{2^n}>0.9\\ {}^n{C}_0\cdot \frac{1}{2^n}<0.1\end{array}$ $\begin{array}{c}\frac{1}{2^n}<0.1\\ 2^n>\frac{1}{0.1}\\ 2^n>10\end{array}$.....(4) The minimum value of n that satisfies the given inequality is 4. Thus, the man should toss the coin 4 or more than 4 times.

Q11. In a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six.Find the expected value of the amount he wins / loses.

Answer. In a throw of a die, the probability of getting a six is $\frac{1}{6}$ and the probability of not getting a 6 is $\frac{5}{6}$. Three cases can occur. (i) If he gets a six in the first throw, then the required probability is $\frac{1}{6}$ . Amount he will receive = Re 1 (ii) If he does not get a six in the first throw and gets a six in the second throw, then probability = $=(\frac{5}{6}\times \frac{1}{6})=\frac{5}{36}$ Amount he will receive = −Re 1 + Re 1 = 0

Q12. Suppose we have four boxes A,B,C and D containing coloured marbles as given below: 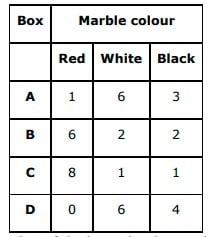 One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box A?, box B?, box C?

Answer. Let R be the event of drawing the red marble. Let EA, EB, and EC respectively denote the events of selecting the box A, B, and C. Total number of marbles = 40 Number of red marbles = 15 $\therefore P\left(R\right)=\frac{15}{40}=\frac{3}{8}$ $\begin{array}{c}\text{Probability of drawing the red marble from box}A\text{is given by}P\left(E_A|R\right)\text{.}\\ \therefore P\left(E_A|R\right)=\frac{P(E_A\cap R)}{P\left(R\right)}=\frac{\frac{1}{40}}{\frac{3}{9}}=\frac{1}{15}\end{array}$ $\begin{array}{c}\text{Probability that the red marble is from box}B\text{is}P\left(E_B|R\right)\text{.}\\ \Rightarrow P\left(E_B|R\right)=\frac{P(E_B\cap R)}{P\left(R\right)}=\frac{\frac{6}{40}}{\frac{3}{8}}=\frac{2}{5}\end{array}$ $\begin{array}{c}\text{Probability that the red marble is from box}C\text{is}P\left(E_C|R\right)\\ \Rightarrow P\left(E_C|R\right)=\frac{P(E_C\cap R)}{P\left(R\right)}=\frac{\frac{8}{40}}{\frac{3}{8}}=\frac{8}{15}\end{array}$

Q13. Assume that the chances of a patient having a heart attack is 40%. It is also assumed that a meditation and yoga course reduce the risk of heart attack by 30% and prescription of certain drug reduces its chances by 25%. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?

Answer. Let A, $E_1$, and $E_2$ respectively denote the events that a person has a heart attack, the selected person followed the course of yoga and meditation, and the person adopted the drug prescription. $\begin{array}{c}\therefore P\left(A\right)=0.40\\ P\left(E_1\right)=P\left(E_2\right)=\frac{1}{2}\\ P\left(A|E_1\right)=0.40\times 0.70=0.28\\ P\left(A|E_2\right)=0.40\times 0.75=0.30\end{array}$ Probability that the patient suffering a heart attack followed a course of meditation and yoga is given by P (E1|A). $\begin{array}{cc}P\left(E_1|A\right)& =\frac{P\left(E_1\right)P\left(A{E}_1\right)}{P\left(E_1\right)P\left(A|E_1\right)+P\left(E_2\right)P\left(A|E_2\right)}\\ & =\frac{\frac{1}{2}\times 0.28}{\frac{1}{2}\times 0.28+\frac{1}{2}\times 0.30}\\ & =\frac{14}{29}\end{array}$

Q14. If each element of a second order determinant is either zero or one, what is the probability that the value of the determinant is positive? (Assume that the individual entries of the determinant are chosen independently, each value being assumed with probability 1/2 ).

Answer. The total number of determinants of second order with each element being 0 or 1 is $(2{)}^4$ = 16 The value of determinant is positive in the following cases. $\left|\begin{array}{cc}1& 0\\ 0& 1\end{array}\right|\left|\begin{array}{cc}1& 1\\ 0& 1\end{array}\right|\left|\begin{array}{cc}1& 0\\ 1& 1\end{array}\right|$ Required probability = Required probability

Q15. An electronic assembly consists of two subsystems, say, A and B. From previous testing procedures, the following probabilities are assumed to be known: P(A fails) = 0.2 P(B fails alone) = 0.15 and P(A and B fail) = 0.15 ,Evaluate the following probabilities (i) P(A fails|B has failed) (ii) P(A fails alone)

Answer. Let the event in which A fails and B fails be denoted by. Let the event in which A fails and B fails be denoted by $\begin{array}{c}P\left(E_A\right)=0.2\\ P(E_A,E_B)=0.15\end{array}$ $\begin{array}{c}P\left(B\text{fails alone}\right)=P\left(E_B\right)-P\left(E_A{E}_B\right)\\ 0.15=P\left(E_B\right)-0.15\\ P\left(E_B\right)=0.3\\ \left(i\right)P\left(E_A|E_B\right)=\frac{P(E_A\cap E_B)}{P\left(E_B\right)}=\frac{0.15}{0.3}=0.5\\ \text{(ii)}P\left(\text{A fails alone}\right)=P\left(E_A\right)-P\left(E_A{E}_B\right)\\ =0.2-0.15\\ =0.05\end{array}$

Q16. Bag I contains 3 red and 4 black balls and Bag II contains 4 red and 5 black balls. One ball is transferred from Bag I to Bag II and then a ball is drawn from Bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred ball is black. Choose the correct answer in each of the following:

Answer. Let E1 and E2 respectively denote the events that a red ball is transferred from bag I to II and a black ball is transferred from bag I to II. $\begin{array}{c}P\left(E_1\right)=\frac{3}{7}\text{and}P\left(E_2\right)=\frac{4}{7}\\ \text{Let}A\text{be the event that the ball drawn is red.}\\ \text{When a red ball is transferred from bag I to II,}\\ P\left(A|E_1\right)=\frac{5}{10}=\frac{1}{2}\\ \text{when a black ball is transferred from bag I to II,}\\ P\left(A|E_2\right)=\frac{4}{10}=\frac{2}{5}\end{array}$ $\begin{array}{cc}\therefore P\left(E_2|A\right)& =\frac{P\left(E_2\right)P\left(A|E_2\right)}{P\left(E_1\right)P\left(A|E_1\right)+P\left(E_2\right)P\left(A|E_2\right)}\\ & =\frac{4}{7}\times \frac{2}{5}\\ & \frac{3}{7}\times \frac{1}{2}+\frac{4}{7}\times \frac{2}{5}\\ & =\frac{16}{31}\end{array}$

Q17. If A and B are two events such that P(A) ≠ 0 and P(B | A) = 1, then (A) A ⊂ B (B) B ⊂ A (C) B = φ (D) A = φ

Answer. $\begin{array}{c}P\left(A\right)\ne 0\text{and}P\left(B|A\right)=1\\ P\left(B|A\right)=\frac{P(B\cap A)}{P\left(A\right)}\\ I=\frac{P(B\cap A)}{P\left(A\right)}\\ P\left(A\right)=P(B\cap A)\\ \Rightarrow A\subset B\\ \text{Thus, the correct answer is A.}\end{array}$

Q18. If P(A|B) > P(A), then which of the following is correct : (A) P(B|A) < P(B) (B) P(A ∩ B) < P(A) . P(B) (C) P(B|A) > P(B) (D) P(B|A) = P(B)

Answer. $\begin{array}{c}P\left(A|B\right)>P\left(A\right)\\ \Rightarrow \frac{P(A\cap B)}{P\left(B\right)}>P\left(A\right)\\ \Rightarrow P(A\cap B)>P\left(A\right)\cdot P\left(B\right)\\ \Rightarrow \frac{P(A\cap B)}{P\left(A\right)}>P\left(B\right)\\ \Rightarrow P\left(B|A\right)>P\left(B\right)\end{array}$ Thus, the correct answer is C.

Q19. If A and B are any two events such that P(A) + P(B) – P(A and B) = P(A), then (A) P(B|A) = 1 (B) P(A|B) = 1 (C) P(B|A) = 0 (D) P(A|B) = 0

Answer. $\begin{array}{c}P\left(A\right)+P\left(B\right)-P\left(A\text{and}B\right)=P\left(A\right)\\ \Rightarrow P\left(A\right)+P\left(B\right)-P(A\cap B)=P\left(A\right)\\ \Rightarrow P\left(B\right)-P(A\cap B)=0\\ \Rightarrow P(A\cap B)=P\left(B\right)\\ \therefore P\left(A|B\right)=\frac{P(A\cap B)}{P\left(B\right)}=\frac{P\left(B\right)}{P\left(B\right)}=1\end{array}$ Thus, the correct answer is B.