NCERT Solutions Class 9 गणित Chapter-7 (त्रिभुज)
Class 9 गणित
पाठ-7 (त्रिभुज)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
प्रश्नावली 7.1
प्रश्न 1.
चतुर्भुज ACBD में, AC = AD है और रेखाखण्ड AB, ∠A को समद्विभाजित करता है। दर्शाइए कि ∆ABC = ∆ABD है। BC और BD के बारे में आप क्या कह सकते हैं?
हल :
दिया है : ACBD एक चतुर्भुज है जिसमें भुजा AC = AD है और रेखाखण्ड AB, ∠A को समद्विभाजित करता है।
सिद्ध करना है : ∆ABC = ∆ABD; और
ज्ञात करना है : BC और BD में सम्बन्ध।
उपपत्ति: ∆ABC और ∆ABD की तुलना करने पर,
AC = AD (दिया है)
∠CAB = ∠DAB (दिया है)।
AB = AB (उभयनिष्ठ है)
∆ABC = ∆ABD (S.A.S. से)
Proved.
BC = BD
प्रश्न 2.
ABCD एक चतुर्भुज है जिसमें AD = BC और ∠DAB = ∠ CBA है। सिद्ध कीजिए कि
(i) ∆ABD = ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
हल :
दिया है : चतुर्भुज ABCD में AD = BC और ∠DAB = ∠CBA
सिद्ध करना है :
(i) ∆ABD = ∆BAC
(ii) BD = AC
(iii) ∠ ABD = ∠BAC
उपपत्ति (i) ∆ABD और ∆BAC में,
AD = BC (दिया है)
∠DAB = ∠CBA (दिया है)
AB = AB (उभयनिष्ठ है)
∆ABD = ∆BAC (S.A.S. से)
(ii) सर्वांगसम त्रिभुजों में संगत मापें बराबर होती हैं और ∆ABD और ∆BAC सर्वांगसम हैं।
संगत भुजाएँ BD = AC
(iii) ∆ABD = ∆BAC
∠ABD = ∠BAC (C.P.C.T.) Proved.
प्रश्न 3.
एक रेखाखण्ड AB पर AD और BC दो बराबर लम्ब रेखाखण्ड हैं। दर्शाइए कि CD, रेखाखण्ड AB को समद्विभाजित करता है।
हल :
दिया है : AB एक रेखाखण्ड है जिसके सिरों A तथा B पर क्रमश: AD और BC लम्ब इस प्रकार हैं कि AD = BC
सिद्ध करना है : CD, रेखाखण्ड AB को समद्विभाजित करता है।
उपपत्ति: प्रश्नानुसार, ∠DAB = 90° ⇒ ∠ DAO = 90°
तथा ∠CBA = 90° ⇒ ∠CBO = 90°
∠DAO = ∠CBO …(1)
∠AOD = ∠COB …(2) (शीर्षाभिमुख कोण)
(1) और (2) को जोड़ने पर,
∠DAO + ∠AOD = ∠CBO + ∠COB
⇒ 180° – ∠ADO = 180° – ∠BCO (त्रिभुज के अन्त:कोणों का योग 180° होता है।)
⇒ ∠ODA = ∠OCB …(3)
अब ∆AOD व ∆BOC में,
∠DAO = ∠CBO [समीकरण (1) से]
AD = BC (दिया है)
∠ODA = ∠OCB [ समीकण (3) से]
∆AOD = ∆BOC (S.A.S. से)
AO = BO (C.P.C.T.)
रेखाखण्ड AB बिन्दु O पर समद्विभाजित होता है।
अत: CD, रेखाखण्ड AB को बिन्दु0 पर समद्विभाजित करता है।
Proved.
प्रश्न 4.
l और m दो समान्तर रेखाएँ हैं जिन्हें समान्तर रेखाओं pऔर qका एक अन्य युग्म प्रतिच्छेदित करता है। दर्शाइए कि ∆ABC = ∆CDA
हल:
दिया है। l और m दो समान्तर रेखाएँ हैं जिनको एक अन्य दो समान्तर रेखाओं p और q का युग्म बिन्दुओं A, B, C और D पर प्रतिच्छेदित करता है। रेखाखण्डे AC खींचा गया है।
सिद्ध करना है : ∆ABC = ∆CDA
उपपत्ति : l || m और AC एक तिर्यक रेखाखण्ड इन्हें प्रतिच्छेदित करता है।
∠DAC = ∠ BCA (एकान्तर कोण युग्म)
इसी प्रकार, p || q है और AC एक तिर्यक रेखाखण्ड इन्हें प्रतिच्छेदित करता है।
∠DCA = ∠BAC (एकान्तर कोण युग्म)
अब ∆ABC और ∆CDA में, ∠BCA = ∠DAC (ऊमर सिद्ध किया है)
AC = AC (उभयनिष्ठ है)
∠BAC = ∠DCA (ऊपर सिद्ध किया है)
∆BC = ∆CDA (A.S.A से)
Proved.
प्रश्न 5.
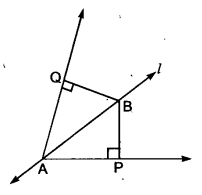
रेखा l कोण A को समद्विभाजित करती है और B रेखा पर स्थित कोई बिन्दु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लम्ब हैं। दर्शाइए कि
(i) ∆APB = ∆AQB
(ii) BP = BQ अर्थात बिन्दु B कोण A की भुजाओं से समदूरस्थ है।
हल :
दिया है। एक रेखा है जो ∠A को समद्विभाजित करती है। रेखा l पर कोई बिन्दु B स्थित है। बिन्दु B से ∠ A की भुजाओं AP और AQ पर क्रमशः BP और BQ लम्ब खींचे गए हैं।
सिद्ध करना है : (i) ∆APB = ∆AQB,
(ii) BP = BQ अर्थात् बिन्दु B कोण ∆की भुजाओं से समदूरस्थ है।
उपपत्ति : (i) BP ⊥ AP और BQ ⊥ AQ
∠P = 90° और ∠Q = 90° …(1)
A रेखा l, ∠A को समद्विभाजित करती है।
∠QAB = ∠PAB
∠QAB= ∠PAB = x° …(2)
तब ∆APB और ∆AQB के अन्त:कोणों के योग की समानता से,
∠ABP + ∠PAB + ∠P = ∠ABQ + ∠QAB + ∠Q
∠ABP + x + 90° = ∠ABQ + x° + 90° [समीकरण (1) तथा (2) से]
∠ABP =∠ABQ
Proved.
अब ∆APB और ∆AQB में, ∠PAB = ∠QAB (दिया है)
AB = AB (उभयनिष्ठ है)
∠ABP = ∠ABQ (अभी सिद्ध किया है)
∆APB = ∆AQB (A.S.A से)
(ii) : ∆APB = ∆AQB
BP= BQ (C.P.C.T.)
अर्थात बिन्दु B, ∠A की भुजाओं से समदूरस्थ है।
Proved.
प्रश्न 6.
दी गई आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है, दर्शाइए कि BC = DE है।
हल :
दिया है : दी गई आकृति के ∆ABD में AB = AD तथा ∆ACE में AC = AE है और ∠BAD = ∠EAC। रेखाखण्ड DE खींचा। गया है।
सिद्ध करना है : BC = DE
उपपत्ति : ∠ BAD = ∠ EAC दोनों ओर ∠DAC जोड़ने पर,
∠BAD + ∠DAC = ∠EAC + ∠DAC
∠BAC = ∠DAE
अब ∆ABC तथा ∆ADE में,
AB = AD (दिया है)
∠BAC = ∠DAE [समीकरण (1) से]
AC = AE (दिया है)
∆ABC = ∆DE (S.A.S. से)
अतः BC = DE (C.P.C.T.)
Proved.
प्रश्न 7.
AB एक रेखाखण्ड है और Pइसका मध्य बिन्दु है। D और E रेखाखण्ड AB के एक ही ओर स्थित दो बिन्दु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। दर्शाइए कि
(i) ∆DAP = ∆EBP
(ii) AD = BE
हल :
दिया है : AB एक रेखाखण्ड है जिसका मध्य-बिन्दु P है। AB के एक ही ओर दो बिन्दु D और E हैं। D से रेखाखण्ड DA और DP खींचे गए हैं और E से रेखाखण्ड EB और EP खींचे गए हैं जिससे ∠BAD = ∠ABE तथा ∠EPA = ∠DPB है।
सिद्ध करना है :
(i) ∆DAP = ∆EBP
(ii) AD = BE
उपपत्ति (i) P, AB का मध्य बिन्दु है जिससे AP= BP
और ∠BAD = ∠ABE (दिया है)
∠PAD = ∠PBE
हमें ज्ञात है कि ∠EPA = ∠DPB
दोनों पक्षों में ∠EPD जोड़ने पर,
∠EPA + ∠ EPD = ∠DPB + ∠EPD
∠DPA = ∠EPB (चित्र से)
अब ∆DAP तथा ∆EBP में, ∠DPA = ∠ EPB (अभी सिद्ध किया है)
AP = BP (P, AB का मध्य-बिन्दु है)
∠PAD = ∠PBE (सिद्ध कर चुके हैं)
∆DAP = ∆EBP (A.S.A. से)
(ii) ∆DAP = ∆EBP
AD = BE (C.P.C.T.)
Proved.
प्रश्न 8.
एक समकोण त्रिभुज ABC में, जिसमें ∠C समकोण है, M कर्ण AB का मध्य बिन्दु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिन्दु D को बिन्दु B से मिला दिया जाता है। दर्शाइए कि :
(i) ∆AMC = ∆BMD
(ii) ∠DBC एक समकोण है।
(iii) ∆DBC = ∆ACB
(iv) CM = AB
हल :
दिया है: ABC एक समकोण त्रिभुज है जिसमें ∠C = 90° है तथा कर्ण AB को मध्य-बिन्दु M है। रेखाखण्ड CM खींचकर इसे बिन्दु D तक इस प्रकार बढ़ाया गया है कि CM = DM है। बिन्दु D को बिन्दु B से मिलाकर रेखा BD खींची गई है।
सिद्ध करना है :
(i) ∆AMC = ∆BMD
(ii) ∠DBC एक समकोण है।
(iii) ∆DBC = ∆ACB
(iv) CM = AB
उपपत्ति : (i) ∆AMC और ∆BMD में,
AM = BM (M, AB का मध्य-बिन्दु है)
∠AMC = ∠BMD (शीर्षाभिमुख कोण)
CM = DM (दिया है)
∆AMC = ∆BMD (S.A.S. से)
(ii) ∆AMC = ∆BMD
∠MAC = ∠ MBD
AC || BD
∠DBC + ∠ACB = 180°
∠DBC + 90° = 180°
(iii) ∆DBC और ∆ACB में,
DB = AC (C.P.C.T.) [∆AMC = ∆BMD]
∠DBC = ∠ACB [ भाग (ii) से ]
BC = BC (उभयनिष्ठ)
∆DBC = ∆ACB (S.A.S. से)
(iv) DC = AB (C.P.C.T.)
2CM = AB (DM = CM)
CM = AB
Proved.
प्रश्नावली 7.2
प्रश्न 1.
एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। A और O को जोड़िए और दर्शाइए कि
(i) OB = OC
(ii) AO, ∠A को समद्विभाजित करता है।
हल :
दिया है : समद्विबाहु ∆ABC में, AB = AC है।
∠B और ∠C के समद्विभाजक BO तथा CO बिन्दु O पर मिलते हैं। रेखाखण्ड AO को जोड़ा गया है।
सिद्ध करना है :
(i) OB = OC
(ii) AO, ∠A को समद्विभाजित करता है।
उपपत्ति :
(i) ∆ABC में, AC = AB (दिया है)
∠ABC = ∠ACB
(त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं)
∠ABC =
∠ACB
∠OBC = ∠OCB …(1) (BO, CO क्रमशः ∠B और ∠C के समद्विभाजक हैं) :
∆OBC में,
∠OBC = ∠OCB
अतः OB = OC (त्रिभुज में समान कोणों की सम्मुख भुजाएँ समान होती हैं।)
(ii) ∆ABO तथा ∆ACO में,
AB = AC (दिया है)
OB = OC (ऊपर सिद्ध किया है)
AO = AO (उभयनिष्ठ भुजा है)
∆ABO = ∆ACO (S.S.S. से)
∠BAO = ∠CAO (C.P.C.T.)
अर्थात, AO, ∠A को समद्विभाजित करता है।
Proved.
प्रश्न 2.
∆ABC में AD भुजा BC का लम्ब समद्विभाजक है दर्शाइए कि ∆ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
हल :
दिया है : ABC एक त्रिभुज है जिसमें भुजा BC का लम्ब समद्विभाजक AD है।
सिद्ध करना है : ∆ABC समद्विबाहु त्रिभुज है जिसमें AB = AC है।
उपपत्ति : AD, BC का लम्ब समद्विभाजक है।
BD = CD तथा ∠ADB = ∠ADC = 90°
अब ∆ABD और ∆ACD में,
BD = CD (ऊपर सिद्ध किया है)
∠ADB = ∠ADC (ऊपर सिद्ध किया है)
AD = AD (उभयनिष्ठ भुजा है)
∆ABD = ∆ACD (S.A.S.से)
AB = AC (C.P.C.T.)
अर्थात् ∆ABC समद्विबाहु है।
Proved.
प्रश्न 3.
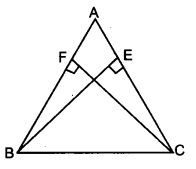
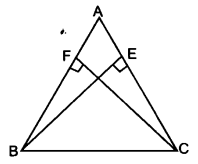
ABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमशः शीर्षलम्ब BE तथा CF खींचे गए हैं। दर्शाइए कि ये शीर्ष लम्ब बराबर हैं।
हल :
दिया है : एक समद्विबाहु ∆ABC में AB = AC तथा शीर्ष B से भुजा AC पर BE लम्ब डाला गया है और शीर्ष C से भुजा AB पर CF लम्ब डाला। गया है।
सिद्ध करना है : BE = CF
उपपत्ति: ∆ABC में,
AC = AB (दिया है)
∠ABC = ∠ACB … (1) (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं)
अब ∆BCF और ∆CBE में,
∠ BFC = ∠CEB (BE ⊥ AC तथा CF ⊥ AB)
BC = BC (उभयनिष्ठ भुजा)
∠FBC = ∠ ECB (∠ABC = ∠FBC तथा ∠ACB = ∠ECB)
∆BCF = ∆CBE (A.S.A. से)
BE = CF (C.P.C.T.)
Proved.
अर्थात दोनों शीर्षलम्ब बराबर हैं।
प्रश्न 4.
ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलम्ब BE तथा CF बराबर हैं। दर्शाइए कि
(i) ∆ABE = ∆ACF
(ii) AB = AC अर्थात ∆ABC एक समद्विबाहु त्रिभुज है।
हल :
दिया है : ∆ABC में शीर्ष B से शीर्षलम्ब BE तथा शीर्ष C से शीर्षलम्ब CF, क्रमशः AC और AB पर इस प्रकार खींचे गए हैं कि BE = CF है।
सिद्ध करना है :
(i) ∆ABE = ∆ACF
(ii) AB = AC अर्थात ∆ABC समद्विबाहु है।
उपपत्ति : (i) BE शीर्षलम्ब है AC पर ∠AEB = 90°
∠ABE = 90° – A (त्रिभुज के अन्त:कोणों को योग 180° होता है)
इसी प्रकार, CF शीर्षलम्ब है AB पर
∠AFC = 90°
∠ACF = 90° – A ( त्रिभुज के अन्त:कोणों का योग 180° होता है)
∠ABE = ∠ACF …….(1)
अब ∆ABE और ∆ACF में,
∠ABE = ∠ACF [समीकरण (1) से]
BE = CF (दिया है)
∠AEB= ∠AFC (प्रत्येक 90°)
∆ABE = ∆ACF (A.S.A.से)
(ii) ∆ABE = ∆ACF
AB = AC (C.P.C.T.)
अत: ∆ABC समद्विबाहु है।
Proved.
प्रश्न 5.
ABC और DBC समान (एक ही) आधार पर स्थित दो समद्विबाहु त्रिभुज हैं। दर्शाइए कि ∠ABD = ∠ACD
हल :
दिया है। दो समद्विबाहु ∆ABC और ∆DBC एक ही आधार BC पर स्थित हैं और AB = AC तथा DB = DC
सिद्ध करना है : ∠ABD = ∠ACD
उपपत्ति : ∆ABC में,
AB = AC (दिया है)
∠ACB = ∠ABC (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं) …(1)
पुनः ∆DBC में, DB = DC (दिया है)
∠BCD = ∠CBD (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं) …(2)
समीकरण (1) व (2) को जोड़ने पर,
∠ ACB + ∠BCD = ∠ABC + ∠CBD
∠ACD = ∠ABD
अतः ∠ABD = ∠ACD
Proved.
प्रश्न 6.
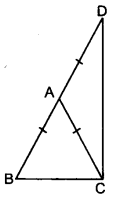
ABC एक समद्विभाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिन्दु D तक इस प्रकार बढ़ाई गई है कि AD = AB है। दर्शाइए कि ∠BCD एक समकोण है।
हल :
दिया है : ∆ABC एक समद्विबाहु त्रिभुज है जिसमें भुजा AB = AC है और भुजा BA को , बिन्दु D तक इस प्रकार बढ़ाया गया है कि AD = AB है।
सिद्ध करना है : ∠BCD एक समकोण है।
उपपत्ति : ∆ABC में,
AC = AB (दिया है)
∠ABC = ∠ACB (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं) …(1)
भुजा BA को बिन्दु D तक इस प्रकार बढ़ाया गया है कि
AB = AD
परन्तु दिया है कि AB = AC भी हैं।
AC = AD
∆ACD में,
∠ADC = ∠ACD (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं) …(2)
समीकरण (1) व समीकरण (2) को जोड़ने पर,
∠ABC + ∠ADC = ∠ACB + ∠ACD
∠ABC + ∠ADC = ∠ BCD (चित्र से)
∠DBC +∠BDC = ∠BCD (∠ ABC = ∠ DBC तथा ∠ ADC = ∠BDC) …(3)
अब : ∆BCD में,
∠DBC + ∠BDC + ∠BCD = 180° (त्रिभुज के अन्त:कोणों का योग 180° होता है)
∠BCD + ∠BCD = 180° [ समीकरण (3) से]
2 ∠BCD = 180°
∠BCD = 90°
अतः ∠BCD एक समकोण है।
Proved.
प्रश्न 7.
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
हल :
दिया है : ABC एक समकोण त्रिभुज है जिसमें A = 90° और बराबर भुजाओं में AB = AC है।
ज्ञात करना है : ∠B तथा ∠C
गणना : ∆ABC समद्विबाहु है जिसमें AB = AC है।
∠C = ∠B (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं) …(1)
त्रिभुज के अन्त:कोणों का योग 180° होता है।
∠A + ∠B + ∠C = 180°
90° +∠B + ∠B = 180° [समीकरण (1) से]
2 ∠B = 180° – 90° = 90°
∠B = 45° …(1)
∠C = ∠ B
∠C = 45°
अतः ∠B = 45° तथा ∠C = 45°
प्रश्न 8.
दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।
हल :
दिया है : ABC एक समबाहु त्रिभुज है जिसमें भुजाएँ AB, BC और CA परस्पर समान लम्बाई की हैं।
∠A, ∠B और ∠C समबाहु त्रिभुज के अन्त: कोण हैं।
सिद्ध करना है : त्रिभुज का प्रत्येक अन्त:कोण = 60°
उपपत्ति: ∆ABC समबाहु है जिसमें AB = BC = AC
यदि AB = AC तो ∠C = ∠B …..(1)
यदि AB = BC तो ∠C = ∠A …(2) (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं)
समीकरण (1) व समीकरण (2) से
∠A = ∠B = ∠C …(3)
परन्तु त्रिभुज के अन्त:कोणों का योग = 180°
∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠A + ∠A = 180°
⇒ 3 ∠A = 180°
⇒ ∠A = 60°
तब समीकरण (3) से
∠A = ∠B = ∠C = 60°
अतः समबाहु त्रिभुज का प्रत्येक अन्त: कोण = 60°
Proved.
प्रश्नावली 7.3
प्रश्न 1.
∆BC और ∆DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D, भुजा BC के एक ही ओर स्थित हैं। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे तो दर्शाइए कि :
(i) ∆ABD = ∆ACD
(ii) ∆ABP = ∆ACP
(iii) AP, ∠A और ∠D दोनों को समद्विभाजित करता है।
(iv) AP, रेखाखण्ड BC का लम्ब समद्विभाजक है।
हल :
दिया है। एक ही आधार BC पर दो समद्विबाहु त्रिभुज, ∆ABC और ∆DBC ऐसे स्थित हैं कि A और D, BC के एक ही ओर हैं।
AD को बढ़ाने पर यह BC को P पर काटती है।
सिद्ध करना है :
(i) ∆ABD = ∆ACD
(ii) ∆ABP = ∆ACP
(iii) AP, ∠A और ∠D दोनों को समद्विभाजित करता है।
(iv) AP, रेखाखण्ड BC का लम्ब समद्विभाजक है।
उपपत्ति : ∆ABC समद्विबाहु है जिसको आधार BC है।
AB = AC
और ∆DBC समद्विबाहु है जिसका आधार BC है।
BD = CD
(i) ∆ABD और ∆ACD में,
AB = AC [समीकरण (1) से]
BD = CD [समीकरण (2) से ]
AD = AD (उभयनिष्ठ भुजा से)
∆ABD = ∆ACD (S.S.S. से)
(ii) ∆ABD = ∆ACD
∠BAD = ∠CAD
अर्थात् AD, ∠A का समद्विभाजक है। (C.P.C.T.)
तबे AD को आगे बढ़ाने पर AP भी ∠A का समद्विभाजक होगा।
अब ∆ABP और ∆ACP में,
AB = AC [समीकरण (1) से]
∠BAP = ∠CAP ( AP, ∠A का समद्विभाजक है।)
AP = AP (उभयनिष्ठ भुजा)
∆ABP = ∆ACP (S.A.S. से)
(iii) ∆ABP = ∆ACP के ∠BDP = ∠CDP (C.P.C.T.)
DP, ∠D का समद्विभाजक है।
AP, ∠D का समद्विभाजक है। और हम अभी सिद्ध कर चुके हैं कि AP, ∠A का समद्विभाजक है।
तब, AP, ∠A और ∠D दोनों को समद्विभाजित करता है।
(iv) अभी हमने सिद्ध किया है कि ∆ABP = ∆CP
∠APB = ∠APC
तथा BP = CP (C.P.C.T.)
अब BP = CP
AP, भुजा BC का समद्विभाजक है।
∠ APB + ∠ APC = 180° और ∠APB = ∠APC (रेखीय युग्म)
तब हल करने पर,
∠APB = ∠APC = 90°
AP, BC पर लम्ब है।
AP, BC पर लम्ब भी है और AP, BC का समद्विभाजक भी है।
अतः AP रेखाखण्ड BC का लम्ब समद्विभाजक है।
Proved.
प्रश्न 2.
AD एक समद्विबाहु त्रिभुज ABC का शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि
(i) AD, रेखाखण्ड BC को समद्विभाजित करता है।
(ii) AD, ∠A को समद्विभाजित करता है।
हल :
दिया है : ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है।
त्रिभुज के शीर्ष A से BC पर AD लम्ब डाला गया है जिससे AD शीर्षलम्ब है।
सिद्ध करना है :
(i) AD, रेखाखण्ड BC को समद्विभाजित करता है।
(ii) AD, ∠A को समद्विभाजित करता है।
उपपत्ति : AD, ∆ABC का शीर्षलम्ब है।
AD ⊥ BC के ∠ADB = 90°
और ∠ADC = 90°
AB, ∆ABD को और AC, ∆ACD का कर्ण है।
तब समकोण त्रिभुज ABD और समकोण त्रिभुज ACD में, ∠ADB = ∠ADC (प्रत्येक 90°)
AB = AC (दिया है)
AD = AD (उभयनिष्ठ भुजा)
∆ABD = ∆ACD (R.H.S.)
(i) ∆BD = ∆ACD
BD = CD (C.P.C.T.)
D, BC का मध्य-बिन्दु है।
अत: AD, रेखाखण्ड BC को समद्विभाजित करता है।
(ii) ∆ABD = ∆ACD
∠BAD = ∠CAD (C.P.C.T.)
अत: AD, ∠A को समद्विभाजित करता है।
Proved.
प्रश्न 3.
एक ∆BC की दो भुजाएँ AB तथा BC और माध्यिका AM क्रमशः एक-दूसरे ∆PQR की भुजाओं PQ तथा QR और माध्यिका PN के बराबर है। दर्शाइए कि
(i) ∆ABM = ∆PQN
(ii) ∆ABC = ∆PQR
हल :
दिया है: ∆ABC और ∆PQR दो त्रिभुज हैं जिनमें AB = PQ, BC = QR तथा माध्यिका AM = PN
सिद्ध करना है :
(i) ∆ABM = ∆PQN
(ii) ∆ABC = ∆PQR
उपपत्ति : BC = QR (दिया है)=
BM = QN (AM व PN माध्यिकाएँ हैं)
(i) ∆ABM और ∆PQN में,
AB = PQ (दिया है)
AM = PN (दिया है)
BM = QN (ऊपर सिद्ध किया है)
∆ABM = ∆PQN (S.S.S. से)
(ii) ∆ABM = ∆PQN ⇒ ∠B = ∠Q (C.P.C.T.) …(1)
अब ∆BC तथा ∆PVR में,
AB = PQ (दिया है)
BC = QR (दिया है)
∠B = ∠Q [समीकरण (1) से]
अतः ∆BC = APQR (S.A.S. परीक्षण से)
Proved.
प्रश्न 4.
BE और CF एक ∆ABC के दो बराबर शीर्षलम्ब हैं। R.H.S. सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ∆ABC एक समद्विबाहु त्रिभुज है।
हल :
दिया है : ABC एक त्रिभुज है जिसमें शीर्ष B से भुजा AC पर BE शीर्ष लम्ब खींचा गया है और शीर्ष C से भुजा AB पर CF शीर्षलम्ब इस प्रकार है कि BE = CF
सिद्ध करना है: ∆ABC एक समद्विबाहु त्रिभुज है।
उपपत्ति : ∆ABC में BE, शीर्ष B से AC पर शीर्षलम्ब है।
∠BEC = 90°
∆BEC एक समकोण त्रिभुज है जिसमें कर्ण BC है।
पुनः ∆ABC में CF, शीर्ष C से AB पर शीर्षलम्ब है।
∠ BFC = 90°
∆BFC एक समकोण त्रिभुज है जिसमें कर्ण BC है।
समकोण त्रिभुज ∆BEC और ∆BFC में,
∠ BEC = ∠CFB (प्रत्येक 90°)
BE = CF (दिया है)
BC = BC (उभयनिष्ठ भुजा)
∆BEC = ∆BFC (R.H.S.)
∠ECB = ∠ FBC
⇒ ∠ACB =∠ ABC (C.P.C.T.)
अब ∆ABC में,
∠ACB = ∠ABC
AB = AC (त्रिभुज में समाने कोणों की सम्मुख भुजाएँ समान होती हैं)
अतः ∆ABC एक समद्विबाहु त्रिभुज है।
Proved.
प्रश्न 5.
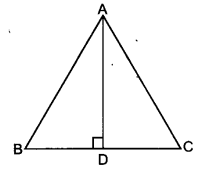
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींचकर दर्शाइए कि ∠B = ∠C
हल :
दिया है: ∆ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है।
शीर्ष A से BC पर AP लम्ब खींचा गया है। सिद्ध करना है : ∠B = ∠C
उपपत्ति: AP⊥ BC
∆APB में, ∠APB = 90° जिससे कर्ण AB है।
और ∆APC में, ∠APC = 90° जिससे कर्ण AC है।
अब ∆APB और ∆APC में,
∠APB = ∠ APC (प्रत्येक 90°)
AB = AC (दिया है)
AP = AP (उभयनिष्ठ भुजा)
∆APB = ∆APC (R.H.S. से)
अतः ∠B = ∠C (C.P.C.T.)
Proved.
प्रश्नावली 7.4
प्रश्न 1.
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लम्बी (या सबसे बड़ी) भुजा होती है।
हल :
दिया है : ∆ABC में, ∠C = 90° तथा भुजा AB कर्ण है।
सिद्ध करना है : कर्ण AB, सबसे बड़ी भुजा है।
उपपत्ति: ∆ABC में, ∠C = 90° (दिया है)
∠A + ∠B = 180° – ∠C = 180° – 90° = 90° (त्रिभुज के अन्त:कोणों का योग 180° होता है)
∠A तथा ∠B, 90° से छोटे हैं।
∠C > ∠A तथा ∠C >∠B
∆ABC में,
∠C > ∠A
AB > BC (प्रमेय-4 से)
∠C > ∠B
AB > CA (प्रमेय-4 से)
AB > BC और AB > CA
AB, दोनों (BC व CA) से बड़ी है।
अतः कर्ण AB सबसे बड़ी भुजा है।
Proved.
प्रश्न 2.
सम्मुख आकृति में, ∆ABC की भुजाओं AB और AC को क्रमशः बिन्दुओं P और Q तक बढ़ाया गया है साथ ही ∠PBC < ∠QCB है। दर्शाइए कि AC > AB
हल :
दिया है : ∆ABC में भुजाओं AB और AC को आगे बढ़ाया गया है। बढ़ी हुई AB पर बिन्दु P और बढ़ी हुई AC पर बिन्दु Q लिया गया है।
इस प्रकार बने बहिष्कोणों में ∠PBC < ∠QCB सिद्ध करना है : AC > AB
उपपत्ति : PBC, ∆ABC का बहिष्कोण है।
∠PBC = ∠ACB +∠A …..(1)
और ∠QCB भी ∆ABC का बहिष्कोण है।
∠QCB = ∠ABC + ∠A …(2)
∠PBC < ∠QCB
∠ACB + ∠A < ∠ABC + ∠A
[समीकरण (1) तथा (2) से
∠ACB < ∠ABC
अब ∆ABC में,
∠ACB < ∠ABC ∠ABC > ∠ACB
AC > AB (बड़े कोण की सम्मुख,भुजा बड़ी होती है)
Proved.
प्रश्न 3.
सम्मुख आकृति में ∠B < ∠A और ∠C < ∠D है। दर्शाइए कि AD < BC
हल :
दिया है : दी गई आकृति में ∆ABO में ∠B < ∠A
और ∆CDO में ∠C < ∠D.
सिद्ध करना है : ऋजु रेखा AD < BC
उपपत्ति: ∆ABO में,
∠B < ∠A
AO < BO (प्रमेय-4 से) …(1)
इसी प्रकार ∆CDO में, ∠C < ∠D
OD < OC (प्रमेय-4 से) …(2) (
1) व (2) को जोड़ने पर,
AO + OD < BO + OC
AD < BC
AD < BC Proved.
प्रश्न 4.
सम्मुख आकृति में, AB और CD क्रमशः एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएँ हैं। दर्शाइए कि ∠A > ∠C और ∠B > ∠D
हल :
दिया है : ABCD एक चतुर्भुज है जिसमें AB सबसे छोटी और CD सबसे बड़ी भुजा है।
सिद्ध करना है : ∠A > ∠C और ∠B > ∠D
रचना : रेखाखण्ड AC तथा BD खींचिए।
उपपत्ति : AB सबसे छोटी भुजा है। तब ∆ABC में,
BC > AB
∠BAC > ∠ACB (प्रमेय-3 से) …(1)
पुनः CD सबसे बड़ी भुजा है।
∆ACD में,
CD > AD
∠DAC > ∠DCA (प्रमेय-3 से) …(2)
(1) व (2) को जोड़ने पर,
∠ BAC + ∠DAC > ∠ACB + ∠DCA
∠BAD > ∠BCD
∠A > ∠C
AB सबसे छोटी भुजा है।
तब ∆ABD में,
AD > AB
∠ABD >∠ADB (प्रमेय-3 से) …(3)
इसी प्रकार, CD सबसे बड़ी भुजा है।
तब ∆BCD में,
CD > BC
∠CBD > ∠BDC (प्रमेय-3 से) …(4)
(3) व (4) को जोड़ने पर,
∠ABD + ∠CBD > ∠ADB + ∠BDC
∠ABC > ∠ADC
∠B > ∠D
Proved.
प्रश्न 5.
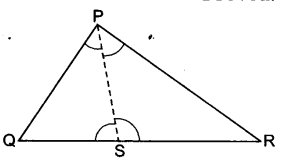
सम्मुख आकृति में, PR > PQ है और PS, ∠QPR को समद्विभजित करता है। सिद्ध कीजिए कि ∠PSR > ∠PSQ है।
हल :
दिया है: ∆PQR में, PR > PQ और ∠QPR को समद्विभाजक, QR से बिन्दु S पर मिलता है।
माना ∠PSR = x° तथा ∠PSQ = y°
सिद्ध करना है : ∠PSR > ∠PSQ
उपपत्ति: ∆PQR में,
PR > PQ
∠Q > ∠R (प्रमेय-3 से)
PS, ∠P को समद्विभाजक है।
∠QPS = ∠P
तथा ∠RPS = ∠P
∠x°, ∆PQS का भुजा QS के बिन्दु S पर बहिष्कोण है।
x°=∠Q + ∠QPS
⇒ ∠Q = x°- ∠QPS
∠Q = x° – ∠P …..(1)
∠y°, ∆PRS का भुजा RS के बिन्दु S पर बहिष्कोण है।
y° = ∠R + ∠RPS
⇒ ∠R = y° – ∠RPS
⇒ ∠R = y° – ∠P
∠Q > ∠R …..(2)
x° – ∠P > y°-
∠P
[समीकरण (1) व (2) से ]
x° > y°
∠PSR > ∠PSQ
Proved.
प्रश्न 6.
दर्शाइए कि एक रेखा पर एक दिए हुए बिन्दु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखण्ड खींचे जा सकते हैं उनमें लम्ब रेखाखण्ड सबसे छोटा होता है।
हल :
दिया है: AB एक सरल रेखा है और P उसके बाहर दिया हुआ एक बिन्दु है। P से रेखा AB पर PM और PN रेखाखण्ड खींचे गए हैं, जिनमें PM ⊥ AB
सिद्ध करना है : PM < PN
उपपत्ति : ∆MPN में, ∠M = 90°, PM ⊥ AB शेष कोण ∠MPN +∠PNM = 90° (त्रिभुज के अन्त:कोणों का योग 180° होता है)
∠PMN सबसे बड़ा कोण है। ∠M > ∠N
PN > PM (प्रमेय-4 से)
अत: P से खींचे रेखाखण्डों में PM सबसे छोटा है।
Proved.
प्रश्नावली 7.5
प्रश्न 1.
ABC एक त्रिभुज है। इसके अभ्यन्तर में एक ऐसा बिन्दु ज्ञात कीजिए जो ∆ABC के तीनों शीर्षों से समदूरस्थ है।
हल :
एक ∆ABC के अभ्यन्तर में एक ऐसा बिन्दु P ज्ञात करना है जो त्रिभुज के तीनों शीर्षों A, B व C से समान दूरी पर हो।
रचना विधि :
(1) सर्वप्रथम दिया हुआ त्रिभुज ABC बनाइए।
(2) AB तथा BC के लम्ब समद्विभाजक खींचिए जो परस्पर बिन्दु P पर काटें।
(3) रेखाखण्ड PA, PB और PC खींचिए।
P अभीष्ट बिन्दु है जो तीनों शीर्षों से समदूरस्थ है।
प्रश्न 2.
किसी त्रिभुज के अभ्यन्तर में एक ऐसा बिन्दु ज्ञात कीजिए जो त्रिभुज की सभी भुजाओं से समदूरस्थ है।
हल :
माना ABC एक त्रिभुज है जिसके अभ्यन्तर में एक ऐसा बिन्दु P ज्ञात करना है जो त्रिभुज की तीनों भुजाओं AB, BC और CA से समदूरस्थ हो।
रचना विधि :
(1) सर्वप्रथम दिया हुआ ∆ABC बनाइए।
(2) ∠B और ∠C के समद्विभाजक खींचिए जो परस्पर बिन्दु P पर काटें।
P अभीष्ट बिन्दु है जो तीनों भुजाओं से समदूरस्थ है।
प्रश्न 3.
एक बड़े पार्क में, लोग तीन बिन्दुओं (स्थानों ) पर केन्द्रित हैं :
A : जहाँ बच्चों के लिए फिसलपट्टी और झूले हैं।
B : जिसके पास मानव निर्मित एक झील है।
C : जो एक बड़े पार्किंग स्थल और बाहर निकलने के रास्ते के निकट है।
एक आइसक्रीम का स्टॉल कहाँ लगाना चाहिए ताकि वहाँ लोगों की अधिकतम संख्या पहुँच सके?
हल :
A, B और C तीन बिन्दु स्थान हैं। आइसक्रीम का स्टॉल लगाने के लिए लोगों की उस पर अधिकतम पहुँच होने के लिए यह आवश्यक है कि स्टॉल तीनों स्थानों से B’ समदूरस्थ हो।
अत: आइसक्रीम स्टॉल लगाने के लिए हमें एक ऐसे स्थान (बिन्दु) P का चयन करना है जो पार्क के तीनों स्थानों से समान दूरी पर हो।
ज्ञात करने की विधिः
(1) बिन्दु ∆से बिन्दु B को, बिन्दु B से बिन्दु C को और बिन्दु C से बिन्दु A को ऋजु रेखाओं द्वारा मिलाकर ∆ABC बनाइए।
(2) किन्हीं दो भुजाओं (AB व BC) के लम्ब समद्विभाजक खींचिए जो परस्पर बिन्दु P पर काटें।
आइसक्रीम स्टॉल के चयन के लिए उपयुक्त स्थान बिन्दु P होगा जो तीनों है स्थानों से समदूरस्थ है।
प्रश्न 4.
घड्भुजीय और तारे के आकार की रंगोलियों को 1 सेमी भुजा वाले समबाहु त्रिभुजों से भरकर पूरा कीजिए। प्रत्येक स्थिति में त्रिभुजों की संख्या गिनिए। किसमें अधिक त्रिभुज हैं?
हल :
चित्रों से स्पष्ट है कि विकर्गों को मिलाने पर षड्भुजीय आकृति को 6 समबाहु त्रिभुजों में और तारे के आकार की आकृति को 1∠समबाहु त्रिभुजों में विभाजित किया जा सकता है जबकि समबाहु त्रिभुजों में प्रत्येक भुजा, 5 सेमी है।
पुनः षड्भुजीय आकृति के एक समबाहु त्रिभुज जिसकी भुजा 5 सेमी है, को 1 सेमी भुजा वाले समबाहु त्रिभुजों में विभाजित कर स्पष्ट किया गया है कि 5 सेमी भुजा वाले एक समबाहु त्रिभुज को 1 सेमी भुजा वाले 25 त्रिभुजों में विभाजित किया जा सकता है।
तब स्थिति 1 : षड्भुजीय रंगोली
इसको 1 सेमी भुजा वाले 6 x 25 = 150 समबाहु त्रिभुजों में बाँटा जा सकता है।
स्थिति 2 : तारे के आकार की रंगोली
5 सेमी भुजा वाले समबाहु त्रिभुजों की संख्या = 12
आकृति में 1 सेमी भुजा वाले समबाहु त्रिभुजों की संख्या = 12 x 25 = 300
स्पष्ट है कि तारे के आकार वाली आकृति में त्रिभुजों की संख्या अधिक है।